Построение апериодических текстур и тайлы Ванга

Одной из важнейших задач в текстурировании и построении синтетических текстур является построение больших непериодических (апериодических) текстур. Одним из простых и изящных способов достижения этого является использование так называемых тайлов Ванга (Wang tiles), названных так по имени математика Хао Ванга.

Отдельные тайлы представляют собой квадраты в которых каждому ребру сопоставлен определенный цвет (см. рис 1).

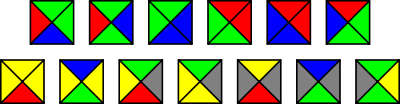
Рис 1. Пример тайлов Ванга.

Используя такие тайлы можно строить замощения плоскости, при этом естественно накладывается условия, чтобы любые два тайла, соприкасающиеся по ребру имели в этом ребре одинаковый цвет (см. рис. 2).

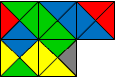
Рис 2. Замощение тайлами Ванга.

Определенными наборами таких тайлов можно замостить всю плоскость, причем доказано, что для некоторых таких наборов (например, для набора с рис. 1) такое замощение может быть только непериодическим.

Существуют довольно простой способ создания тайлов и процедура замощения, дающие всегда непериодическое замощения плоскости. Пусть у нас уже есть как минимум несколько тайлов и мы хотим добавить к имеющимся еще один. Тогда видно, что для выбираемого тайла существует до двух ограничений на пару соседних ребер.

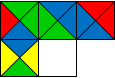
Рис 3. На свободное место можно поставить любой тайл с заданными левым и верхним цветами.

Поэтому если мы выберем такой набор тайлов, чтобы для каждой пары цветов существовало не менее двух тайлов, чтобы цвета их левого и верхнего ребер совпадали с заданными, то у нас всегда будет возможность выбора из как минимум двух тайлов. Сделав этот выбор на основе случайных чисел мы гарантированно получаем непериодическое замощение.

Тем самым, если построить подобный набор тайлов, что каждая пара цветов встречается на смежных ребрах более одного раза, то мы всегда будем иметь возможность выбрать какой именно тайл мы хотим поставить на свободное место. На рисунке 4 приводится набор из 8 подобных тайлов.

Рис 4. Набор из 8 тайлов.

Если у нас есть набор из текстурированных квадратов, то одинаковый цвет на ребрах просто обозначает, что данные тайлы можно по этим ребрам состыковывать без появления видимых артефактов.

Существует красивый способ, позволяющий по фрагменту текстуры создать набор текстурированных тайлов. Для этого вначале из исходной текстуры вырезаются четыре блока одинакового размера, представляющие собой повернутые по 45 градусов квадраты.

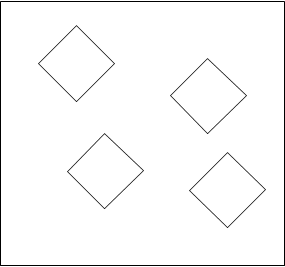
Рис. 5. Вырезаемые блоки из текстуры.

Для получения одного тайла наложим эти четыре блока друг на друга с фиксированным перехлестом, как показано на рис. 6.

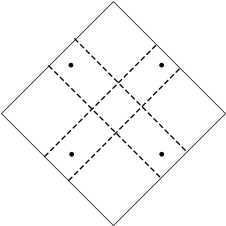
Рис 6. Набор из четырех перекрывающихся текстурированных блоков.

При этом в итоговом блоке у нас будут две полосы, в каждой из которых имеет место перекрытие текстур. Выберем четыре точки в этих полосах, так, что они лежат в вершинах квадрата.

Следующий шаг заключается в том что внутри каждой из этих полос строится непрерывная линия, соединяющая соответствующие точки таким образом, что если просуммировать разность между двумя текстурами для каждого пиксела этой кривой, то получается минимально возможное значение для всех таких кривых.

После того, как в каждой полосе эти кривые построены, осуществим склейку текстур по этим кривым и получим в результате один большой текстурированный блок (см. рис. 7).

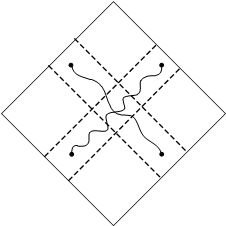
Рис. 7. "Склеенный" из исходных квадратов блок.

Далее по четырем выбранным точкам вырежем из получившегося блока квадрат.

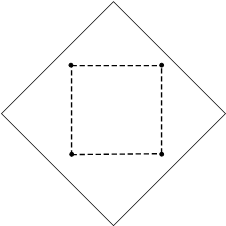
Рис. 8. Вырезанный из блока квадрат.

Обратите внимание, что каждое ребро этого квадрата полностью соответствует одной из исходных текстур.

Теперь мы можем собрать исходные блоки текстуры другим образом, произвести склейку и вырезать еще один квадрат, каждое из ребер которого будет целиком соответствовать одной текстуре. При этом эти квадраты легко могут быть склеены вдоль ребер, соответствующих одной и той же текстуре.

Перебрав все возможные комбинации текстурных блоков мы построим набор тайлов Ванга из которых мы можем строить непериодические текстуры любого желаемого размера.

Рассмотрим теперь, как можно в области перекрытия двух текстур построить кривую, соединяющую две заданные точки и дающую минимальную разницу между текстурами вдоль нее.

Для простоты мы рассмотрим случай, когда перекрытие двух текстурных блоков является горизонтальной полосой (см. рис. 9). Далее мы воспользуемся динамическим программированием для построения соответствующей кривой.

Рис. 9. Построение минимальной кривой, соединяющей две заданные точки.

Итак мы начинаем с исходной точки (x₀,y₀), в которой мы знаем насколько сильно отличаются текстуры t₁ и t₂ между собой.

Далее мы делаем шаг вправо, увеличивая x на единицу. При этом значение y может как измениться на плюс или минус единицу, так и остаться тем же самым. Таким образом мы получаем стоимости соединения точек (x₀+1,y₀+1), (x₀+1,y₀-1) и (x₀+1,y₀) c (x₀,y₀).

Для этих точек мы запоминаем найденную "стоимость" кривой до (x₀,y₀). Далее мы из трех новых точек делаем еще один шаг по x, получая при этом следующие точки - (x₀+2,y₀+2), (x₀+2,y₀+1), (x₀+2,y₀), (x₀+2,y₀-1) и (x₀+2,y₀-2).

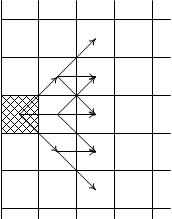
Рис. 10. Пути, ведущие к точкам второй итерации.

Обратите внимание, что в точки (x₀+2,y₀+1) и (x₀+2,y₀-1) можно прийти двумя разными путями, а в точку (x₀+2,y₀) - тремя. Поэтому цену для линий ведущих в эти точки мы будем определять как минимальную из всех способов, какими можно прийти в эти точки.

Таким образом для каждой точки (x_i,y_i) мы будем запоминать минимальную стоимость пути из (x₀,y₀) и координаты предыдущей точки на этом минимальном пути.

Для обработки очередной точки мы смотрим какими путями можно в нее прийти (таких путей всегда будет не более трех) и выбираем из них тот, который обладает минимальной ценой. После этого итоговую цену и координаты предыдущей точки оптимального пути мы запоминаем.

Продолжая этот процесс мы дойдем до конечной точки и тем самым у нас будет готов оптимальный путь соединяющий начальную и конечную точки.

Ниже приводится фрагмент псевдокода, демонстрирующего этот процесс.