Реализация bumpmapping'а - построение базиса касательного пространства, быстрая нормализация векторов

В этой статье мы рассмотрим два важных момента при эффективной реализации попиксельного освещения.

Нахождение базиса касательного пространства для набора треугольников

В рассматриваемых ранее примерах попиксельного освещения с учетом карты нормалей (bumpmap) возникала необходимость задания для каждой вершины всех выводимых граней базиса касательного пространства - векторов t, b и n.

Для случая простой геометрии объекта (например тора), эти вектора легко найти аналитически (что, собственно и делалось ранее). Однако при использовании более сложной геометрии возникает необходимость алгоритма вычисления этих векторов по данным в вершинах.

Проще всего дело обстоит с вектором внешней нормали n - в ряде случаев он просто явно задается для каждой вершины. Если же он не задан, то его легко можно найти по координатам вершин.

Если у нас задан треугольник v₀,v₁,v₂, то нормаль в точке v₀ легко можно найти через векторное произведение ребер:

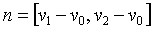
Однако при использовании данной формулы нужно иметь в виду, что она может дать как внешнюю, так и внутреннюю нормаль. Проще всего бороться с этим путем задания для каждого треугольника вершин в таком порядке, чтобы эта формула всегда давала именно внешнюю нормаль.

Обратите также внимание, что эта формула вообще дает нормаль ко всему треугольнику, а не нормаль в какой-то вершине.

Для более точного определения вектора нормали в вершине можно воспользоваться тем, что вершина обычно принадлежит сразу нескольким граням, поэтому для каждой из таких граней вычисляется вектор нормали, а потом они складываются для получения нормали в вершине.

Полученное значение нормали должно быть нормировано для дальнейшего использования.

Для получения двух касательных векторов t и b одной геометрической информации (координат вершин) уже недостаточно и требуется информация о наложении текстурных координат (что вполне естественно, поскольку эти вектора используются именно для корректного наложения карты нормалей).

Рассмотрим сначала идеальный случай - пусть у нас есть гладкая поверхность с заданным на ней законом задания текстурных координат:

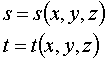
Пусть также задана точка v₀, соответствующая текстурным координатам (s₀,t₀).

Тогда рассмотрим на этой поверхности линии линии, вдоль которых одна из текстурных координат будет постоянна. Нас интересует две таких линии - вдоль одной величина s принимает значение s₀, а вдоль второй величина t принимает значение t₀.

Эти линии проходят через точку v₀ и пересекаются в ней. В случае, когда рассматриваемая поверхность и закон задания текстурных координат являются гладкими и невырожденными в точке v₀, то в этой точке можно построить касательный вектор к каждой из них.

В случае невырожденности закона задания текстурных координат эти вектора будут линейно независимы и если к ним добавить вектор нормали они будут являться базисом касательного пространства в этой точке.

Рассмотрим теперь, как можно найти эти касательные вектора без явного нахождения самих этих линий.

В силу невырожденности закона задания текстурных координат этот закон можно (хотя бы локально, т.е. в малой окрестности точки v₀) обратить, т.е. записать в виде:

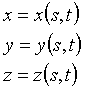
Тогда интересующие нас касательные вектора будут равны (x'_s,y'_s,z'_s,) и (x'_t,y'_t,z'_t,).

Вернемся обратно к треугольнику v₀,v₁,v₂, считая, что в каждой его вершине явно заданы текстурные координаты (s_i,t_i), используемые для обращения к карте нормалей.

Считая, что пространственные и текстурные координаты связаны некоторым законом (рассматриваемого ранее вида), можно приближенно записать следующие разностные отношения:

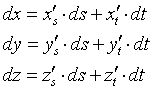
Используя заданные в вершинах треугольника значения пространственных и текстурных координат, можно записать три системы линейных уравнений следующего вида.

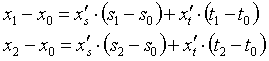
Для решения каждой из этих систем можно с успехом применить известное правило Крамера, т.е. записать интересующие нас производные x'_s,x'_t в виде отношения двух определителей.

Можно упростить запись решения, путем введения следующих двух векторов:

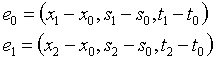
Тогда каждый из необходимых определителей будет являться (с точностью до знака) одной из компонент векторного произведения векторов e0 и e1.

Ниже приводится процедура, реализующая описанный выше алгоритм для вычисления базиса касательного пространства в точке (при этом вектор нормали считается уже найденным).

Обратите внимание, что в конце процедуры проверяется ориентация полученного базиса (она может оказаться как левой так и правой и производится ее коррекция при необходимости).

Для повышения точности, можно вычислить вектора t и b используя несколько треугольников, проходящих через вершину v₀ и взять среднее из полученных значений.

Быстрая нормализация векторов

Способ нормирования векторов с использованием нормирующей кубической карты, хотя и прост, но требует использования текстурного блока и обращения к текстуре.

При использовании фрагментных программ нормирование вектора легко выполняется всего в три команды, однако без фрагментных программ и шейдерных языков высокого уровня, нормирование вектора осуществить довольно сложно.

Однако в ряде случаев можно воспользоваться приближенной формулой, которая для векторов, длины которых не сильно отличаются от единицы, дает достаточно хорошие результаты.

Возьмем за основу известную формулу (основанную на разложении по формуле Тейлора с точностью до первого члена).

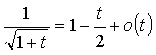
Тогда, если обозначить t=(v,v)-1, то мы получим простую приближенную формулу

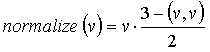
Естественно, что эта формула дает лишь приближенное значение и тем точнее, чем ближе длина вектора v к единице.