

|
Главная
 Статьи
Статьи
 Ссылки
Ссылки
 Скачать
Скачать
 Скриншоты
Скриншоты
 Юмор
Юмор
 Почитать
Почитать
 Tools
Tools
 Проекты
Проекты
 Обо мне
Обо мне
 Гостевая
Гостевая
 Форум
Форум


|
CUDA поддерживает работу с текстурами, предоставляя при этом полный набор функциональности, доступной из графических API. Работа с текстурами в CUDA идет при помощи так называемых текстурных ссылок (texture reference).
Такая ссылка задает некоторую область в памяти, из которой будет производиться чтение. Перед чтением необходимо "привязать" (bind) текстурную ссылку к соответствующей области выделенной памяти.
Текстурная ссылка фактически является объектом, обладающим набором свойств (атрибутов), такими как размерность, размер, тип хранимых данных и т.п. Некоторые из этих свойств можно изменять, другие же являются неизменяемыми и задаются всего один раз.
Текстурная ссылка (texture reference) задается при помощи следующей конструкции:
texturer<Type, Dim, ReadMode> texRef;
Параметр Type обозначает тип данных, возвращаемых при чтении из текстуры. В качестве Type можно использовать базовые целочисленные типы, float, а также все их 1/2/3/4-мерные вектора.
Параметр Dim задает размерность текстуры и принимает значения от 1 до 3 включительно.
Параметр ReadMode определяет нужно ли производить так называемую нормализацию прочитанных из текстуры значений, в тех случаях, когда Type является целочисленным типом (или целочисленным вектором). Нормализацией целочисленных значений называется их отображение в floating-point-значения из отрезка [-1,1] для знаковых типов и из [0,1] для беззнаковых. Фактически нормализация значений - это просто деление на максимально возможное значение данного типа (после преобразования во float).
В качестве значения параметра ReadMode выступает одна из следующих констант - cudaReadModeNormalizedFloat (для случая, когда необходимо произвести нормализацию) и cudaReadModeElementType (когда никакой нормализации проводить не нужно).
К изменяемым атрибутам текстур относятся также какой тип текстурных координат используется (нормализованные или нет), способ адресации (аналог в OpenGL - wrap mode) и тип используемой фильтрации.
В качестве памяти для текстуры можно использовать любую область как линейной памяти (linear memory), так и так называемый CUDA-массив (CUDA array). При этом выбор в качестве памяти линейной памяти накладывает следующие ограничения на текстуру:
Для чтения из текстур, размещенных в линейной памяти, используется функция tex1Dfetch:
template <class Type> Type tex1Dfetch ( texture<Type, 1, cudaReadModeElementType> texRef, int x );
Для чтения из текстур, размещенных в CUDA-массивах используются следующие функции:
template <class Type, enum cudaTextureReadMode readMode> Type tex1D ( texture<Type, 1, readMode> texRef, float x ); template <class Type, enum cudaTextureReadMode readMode> Type tex2D ( texture<Type, 2, readMode> texRef, float x, float y ); template <class Type, enum cudaTextureReadMode readMode> Type tex3D ( texture<Type, 3, readMode> texRef, float x, float y, float z );
Если текстура размещена в линейной памяти, то для выделения и освобождения этой памяти используются рассмотренные в предыдущей статье функции cudaMalloc и cudaFree.
Выделение и освобождения CUDA-массивов производится при помощи функций cudaMallocArray и cudaFreeArray. При выделении памяти как CUDA-массива в функцию cudaMallocArray необходимо кроме размера передать ссылку на структуру cudaChannelFormatDesc, используемую для описания структуры текстуры.
cudaChannelFormatDesc chDesc = cudaCreateChannelDesc<float>(); cudaArray * array; cudaMallocArray ( &array, &chDesc, width, height ); cudaMemcpy2DToArray ( array, 0, 0, devPtr, pitch, width * sizeof ( float ), height, cudaMemcpyDeviceToDevice ); . . . . cudaFreeArray ( array );
В основе типа texture лежит следующая структура:
struct textureReference
{
int normalized;
enum cudaTextureFilterMode filterMode;
enum cudaTextureAddressMode addressMode [3];
struct cudaChannelFormatDesc channelDesc;
};
struct cudaChannelFormatDesc
{
int x, y, z, w;
enum cudaChannelFormatKind f;
};
| Поле | Назначение |
|---|---|
| normalized | Задает происходит ли обращение к данной текстуре с использованием нормализованных текстурных координат (если значение этого поля отлично от нуля) или нет. |
| filterMode | Задает способ фильтрации для текстуры. Допустимыми значениями являются cudaFilterModePoint (аналог в OpenGL - GL_NEAREST) и cudaFilterModeLinear (GL_LINEAR). Обратите внимание, что линейная фильтрация поддерживается только для текстур, возвращающих floating-point-значения. |
| addressMode | Задает режим приведения (wrap mode в OpenGL) для каждой из компонент текстурных координат. Возможными значениям являются cudaAddressModeClamp и cudaAddressModeWrap. |
| channelDesc | Задает формат значения, возвращаемого при чтении из текстуры. Поля x, y, z и w содержат число бит на соответствующую компоненту, а f задает тип данных для этих компонент и принимает одно из следующих значений - cudaChannelFormatKindSigned, cudaChannelFormatKindUnsigned и cudaChannelFormatKindFloat. |
Поля normalized, addressMode и filterMode могут быть изменены прямо во время выполнения программы. Обратите внимание, что все они применимы только к текстурам, расположенным в CUDA-массивах.
Для получения cudaChannelFormatDesc по типу T служит следующая функция:
template <class T> struct cudaChannelFormatDesc cudaCreateChannelDesc <T> ();
Прежде, чем ядро сможет читать из текстуры, соответствующая текстурная ссылка должна быть "привязана" (bind) к выделенной памяти (в зависимости от того к какому именно типу памяти идет привязка). По окончании работы, необходимо вызвать функцию cudaUnbindTexture.
cudaError_t cudaBindTexture ( size_t * offset, const struct textureReference * texRef, const void * devPtr,
const struct cudaChannelFormatDesc * desc, size_t size = UINT_MAX );
cudaError_t cudaBindTextureToArray ( const struct textureReference * texRef, const struct cudaArray * array,
const struct cudaChannelFormatDesc * desc );
cudaError_t cudaUnbindTexture ( const struct textureReference * texRef );
Для копирования памяти между CUDA-массивами и линейной памятью и памятью CPU используются следующие функции:
cudaError_t cudaMemcpyFromArray ( void * dst, const struct cudaArray * srcArray, size_t srcX, size_t srcY,
size_t count, enum cudaMemcpyKind kind );
cudaError_t cudaMemcpy2DFromArray ( void * dst, size_t dpitch, const struct cudaArray * srcArray,
size_t srcX, size_t srcY, size_t width, size_t height, enum cudaMemcpyKind kind );
cudaError_t cudaMemcpyToArray ( struct cudaArray * dstArray, size_t dstX, size_t dstY, const void * src, size_t count,
enum cudaMemcpyKind kind );
cudaError_t cudaMemcpy2DToArray ( struct cudaArray * dstArray, size_t dstX, size_t dstY, const void * src,
size_t spitch, size_t width, size_t height, enum cudaMemcpyKind kind );
cudaError_t cudaMemcpyArrayToArray ( struct cudaArray * dstArray, size_t dstX, size_t dstY,
const struct cudaArray * srcArray, size_t srcX, size_t srcY,
size_t count, enum cudaMemcpyKind kind );
cudaError_t cudaMemcpy2DArrayToArray ( struct cudaArray * dstArray, size_t dstX, size_t dstY,
const struct cudaArray * srcArray, size_t srcX, size_t srcY,
size_t width, size_t height, enum cudaMemcpyKind kind );
Фактически вся работа с константной памятью сводится к копированию данных в нее и из нее. Для этого служат следующие две функции.
template <class T> cudaError_t cudaMemcpyToSymbol ( const T& symbol, const void * src, size_t count, size_t offset, enum cudaMemcpyKind kind ); template <class T> cudaError_t cudaMemcpyFromSymbol ( void * dst, const T& symbol, size_t count, size_t offset, enum cudaMemcpyKind kind );
Функция cudaMemcpyToSymbol копирует count байт с адреса src и смещения offset в символ symbol. Функция cudaMemcpyFromSymbol копирует count байт с символа symbol по адресу src со смещением offset.
Ниже приводится фрагмент кода, иллюстрирующий работу с константной памятью в CUDA.
__constant__ float contsData [256]; float hostData [256]; cudaMemcpyToSymbol ( constData, hostData, sizeof ( data ), 0, cudaMemcpyHostToDevice );
В основе архитектуры GPU G80 лежит массив потоковых мультипроцессоров (Streaming Multiprocessor, SM), их количество может меняться для различных GPU (до 16 на GeForce 8800 GTX).
Когда CUDA запускает ядро на выполнение, то все блоки распределяются между потоковыми мультипроцессорами таким образом, что каждый блок назначается на какой-то мультипроцессор. При этом на один мультипроцессор может быть назначено сразу несколько блоков.
Каждый потоковый мультипроцессор включает в себя 8 скалярных процессоров (Scalar Processor, SP), 2 блока для вычисления трансцендентных функций (Special Function Unit, SFU), shared-память (16 Кбайт), регистры (8192 32-битовых регистра), текстурный кэш и кэш константной памяти (см рис 1).
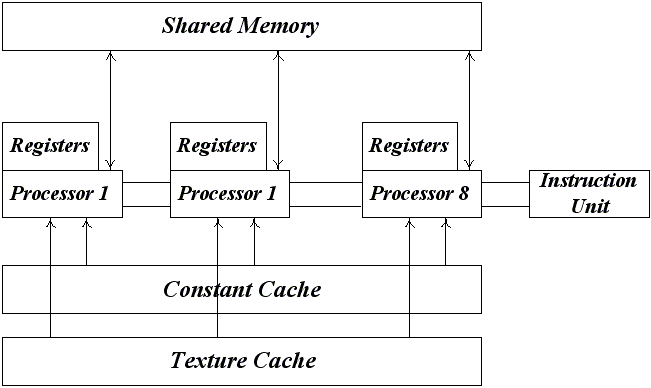
Рис 1. Устройство потокового мультипроцессора.
Мультипроцессор управляет созданием, выполнением и уничтожением нитей (всего на одном мультипроцессоре может выполняться до 768 нитей, до 512 нитей на блок), группируя их в warp'ы по 32 нити. При этом именно warp является единицей управления - для каждого warp'а отслеживается готовы ли данные для его выполнения. На каждом шаге выбирается warp, для которого готовы все данные и выполняется одна команда для всех составляющих его нитей. После этого определяется что нужно данному warp'у для продолжения, выбирается следующий готовый warp и так далее. Важной чертой является то, что весь этот механизм обработки warp'ов не требует никаких специальных расходов (zero overhead).
Обратите внимание, что если внутри одного warp'а происходит ветвление - т.е. для очередного шага часть нитей должна выполнить одну команду, а часть - другую, то warp последовательно выполняет все варианты, блокируя запись для отдельных нитей. Таким образом цена ветвления в пределах warp'а оказывается довольно большой и желательно его избегать.
Количество блоков, которые могут выполняться на одном мультипроцессоре определяется в первую очередь требованиями блока по регистрам и shared-памяти, поскольку они должны разделяться между всеми блоками, выполняющимися на мультипроцессоре.
Так если каждый блок требует для себя 2 Кбайта shared памяти, то на мультипроцессоре можно запустить до 8 блоков.
Быстродействие программ на CUDA определяется двумя факторами - вычислительной производительностью (GFGlops/sec) и скоростью обращения к памяти (GBytes/sec). При этом чаще всего быстродействие ограничивается именно скоростью работы с памятью.
Поэтому для повышения быстродействия программы огромное значение имеет правильная работа с различными типами памяти и учет специфики для каждого из этих типов.
Основными типами памяти на GPU, которые поддерживает CUDA, являются глобальная, shared, текстурная и константная. Два последних типа кэшируются на самом мультипроцессоре и поэтому для них важно только координированность обращений, обеспечивающая высокую эффективность кэша.
Оставшиеся два типа (глобальная и shared) не кэшируются и имеют ряд важных особенностей, учет которых может дать очень большой прирост производительности (в десятки раз).
Глобальная память (GPU DRAM) не кэшируется и поэтому одно обращение к ней может занимать до 600 тактов. Именно оптимизация работы с глобальной памятью может дать огромный прирост производительности.
Обращение к глобальной памяти осуществляется через чтение/запись 32/64/128-битовых слов.
__device__ type dev [32]; // 32 items of type in global memory type data = dev [threadIdx.x]; // reading one item from global memory
Для того, чтобы обращение в глобальную память было скомпилировано в одну команду, важно, чтобы sizeof(type) был равен 4/8/16 байтам и расположение данных было выравнено по sizeof(type) в памяти.
__device__ float data [256]; float3 v; . . . . v = data [i];
Рассмотрим пример выше - размер float3 равен 12 байтам и, поэтому, многие элементы массива data не будут надлежащим образом выровнены. Все это ведет к неэффективному обращению к глобальной памяти. Избежать этого можно несколькими способами.
Простейшим является замена float3 на float4 - хотя мы при этом будем использовать немного больше памяти, но размер каждого элемента массива будет равен 16 байтам и каждый элемент будет выровнен в памяти по 16 байтам. Это позволит скомпилировать каждое обращение к элементу такого массива в одну команду.
Точно такая же ситуация возникает при использовании структур. Если размер структуры превышает 16 байт, то будет произведено несколько обращений к памяти. Для наибольшей эффективности желательно, чтобы размер структуры был кратен 4/8/16 байтам и все экземпляры данной структуры были выровнены в памяти. Так приводимый ниже пример использует опцию __align__ для обеспечения выравнивания в памяти по 16 байтам (что позволит минимизировать число операций чтения/записи).
struct __align__(16)
{
float a;
float b;
float c;
};
Обратите внимание, что вся память GPU, выделяемая при помощи различных запросов, всегда выровнена как минимум по 256 байтам.
Крайне важной особенностью GPU является возможность объединения (coalescing global memory accesses) нескольких запросов в глобальную память в одну операция над блоком (транзакцию). Подобное объединение запросов в один запрос чтения/записи одного блока длиной 32/64/128 байт может происходить в пределах одного half-warp'а. Для того, чтобы такое объединение произошло, должны быть выполнены специальные требования на то, как отдельные нити half-warp'а обращаются к памяти.
Прежде всего получающийся общий блок обязательно должен быть выровнен в памяти(т.е. его адрес должен быть кратен его размеру). Также должны быть выполнены дополнительные требования, зависящие от Compute Capability GPU.
Для GPU с Compute Capability 1.0 и 1.1 объединения запросов в одну транзакцию будет происходит при выполнении следующих условий:
Если нити half-warp'а не удовлетворяют какому-либо из данных условий, то каждое обращение к памяти происходит как отдельная транзакция. На следующих рисунках приводятся типичные паттерны обращения дающие объединения и не дающие объединения.
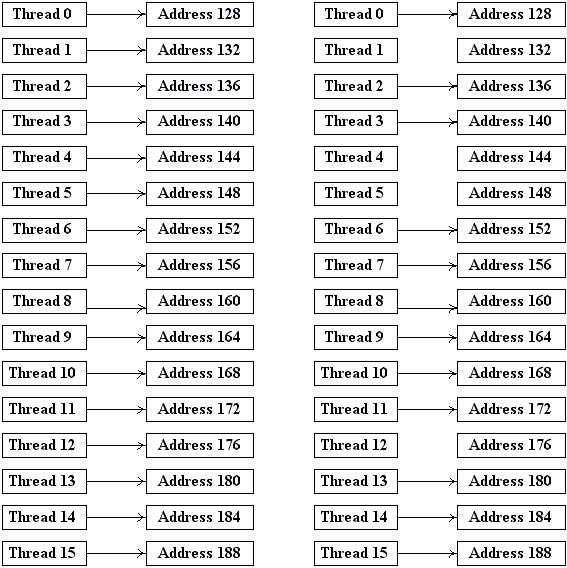
Рис 2. Паттерны обращения к памяти, дающие объединение для Compute Capability 1.0 и 1.1.
На рис. 2 приведены типичные паттерны обращения к памяти, приводящие к объединению запросов в одну транзакцию. Слева у нас выполнены все условия, справа - просто для части нитей пропущено обращение к соответствующим словам (что равно позволяет добавить фиктивные обращения и свести к случаю слева).
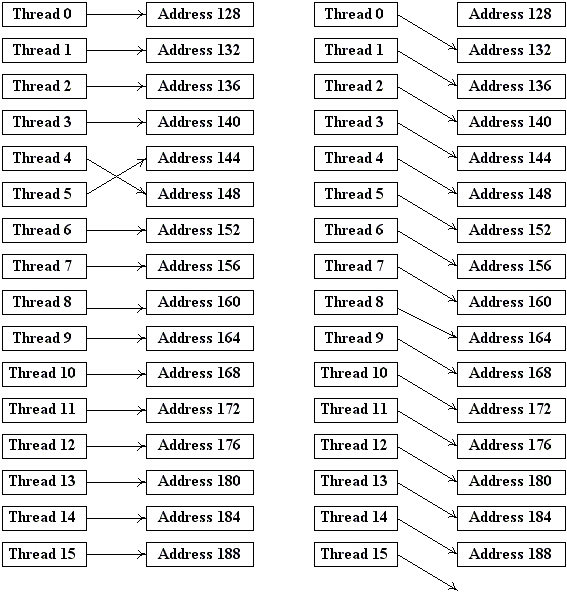
Рис 3. Паттерны обращения к памяти, не дающие объединение для Compute Capability 1.0 и 1.1.
На рис. 3 слева для нитей 4 и 5 нарушен порядок обращения к словам, а справа нарушено условие выравнивание - хотя слова, к которым идет обращения и образуют непрерывный блок из 64 байт, но начало этого блока (по адресу 132) не кратно его размеру (16 байт).
Для GPU с Compute Capability 1.2 и выше объединения запросов в один будет происходить, если слова, к которым идет обращение нитей, лежат в одном сегменте размера 32 байта (если все нити обращаются к 8-битовым словам), 64 байта (если все нити обращаются к 16-битовым словам) и 128 байт (если все нити обращаются к 32-битовым или 64-битовым словам). Получающийся сегмент (блок) должен быть выровнен по 32/64/128 байтам.
Обратите внимание, что в этом случае порядок, в котором нити обращаются к словам, не играет никакой роли и ситуация на рис. 3 слева приведет к объединению всех запросов в одну транзакцию.
Если идет обращения к n соответствующим сегментам, то происходит группировка запросов в n транзакций (только для GPU с Compute Capability 1.2 и выше).
Еще одним моментом работы с глобальной памятью является то, что гораздо эффективнее с точки зрения объединения запросов к памяти является использование не массивов структур, а структуры массивов( отдельных компонент исходной структуры).
struct A __align__(16)
{
float a;
float b;
uint c;
};
A array [1024];
. . .
A a = array [threadIdx.x];
В приведенном выше примере чтение структуры каждой нитью не даст объединения обращений к памяти и на доступ к каждому элементу массива A понадобится отдельная транзакция.
Вместо одного массива A можно сделать три массива его компонент.
float a [1024]; float b [1024]; uint c [1024]; . . . float fa = a [threadIdx.x]; float fb = b [threadIdx.x]; uint uc = c [threadIdx.x];
В результате такого разбиения каждый из трех запросов к очередной компоненте исходной структуры приведет к объединению и в результате нам понадобится всего по три транзакции на half-warp (вместо 16 ранее).
Еще одним важным моментом при работе с глобальной памятью является то, что при большом числе нитей, выполняемых на мультипроцессоре (мультипроцессор поддерживает до 768 нитей), время ожидания warp'ом доступа к памяти может быть использовано для выполнения других warp'ов. Чередование вычислений с обращениями к памяти позволяет более оптимально использовать ресурсы GPU.
Так первому warp'у нужен доступ к памяти. Управление передается другому warp'у, выполняется одна команда для него, далее управление опять передается следующему warp'у и т.д. Для того, чтобы избежать "простоя" мультипроцессора, достаточно обеспечить большое количество warp'ов, которые смогут выполняться в то время, когда первый warp ждет.
Для оптимального доступа к памяти и регистрам желательно, чтобы количество нитей в блоке было кратным 64 и было не менее 192.
Для повышения пропускной способности вся shared-память разбита на 16 банков. Каждый банк работает независимо и если идет обращение к набору слов, лежащий в разных банках, то все эти запросы будут обработаны одновременно.
Если же в сразу несколько нитей обращаются к одному и тому же банку памяти, то происходит конфликт банков (bank conflict) и эти запросы будут выполняться последовательно один за другим (т.е. в несколько раз медленнее).
Банки памяти организованы следующим образом - последовательно идущие 32-битовые слова попадают в последовательно идущие банки. GPU при обращении к shared-памяти независимо обрабатывает запросы от нитей из первого и от второго half-warp'ов. Таким образом нити, принадлежащие разным half-warp'ам не могут вызывать конфликт банков - конфликтовать могут только нити в пределах каждого half-warp'а между собой.
Рассмотрим типичный пример, когда адрес для обращения к памяти линейно зависит от номера нити:
__shared__ float buf [128]; float v = buf [baseIndex + threadIdx.x * s];
При такой схеме обращения к shared-памяти конфликтов не будет только тогда, когда s нечетно. Однако обратите внимание, что если идет доступ к элементам меньшего размера, то ситуация изменяется:
__shared__ char buf [128]; char v = buf [baseIndex + threadIdx.x];
Как легко заметить buf[0], buf[1], buf[2] и buf[3] лежат в одном и том же банке. Поэтому в приведенном выше случае будет иметь место 4-кратный конфликт. Однако его легко можно избежать, поменяв схему обращения к памяти:
__shared__ char buf [128]; char v = buf [baseIndex + threadIdx.x * 4];
На следующем рисунке приведены типичные способы обращения нитей к shared-памяти, когда конфликтов банков не происходит - фактически это означает что существует взаимно-однозначное соответствие между нитями half-warp'а и банками памяти.
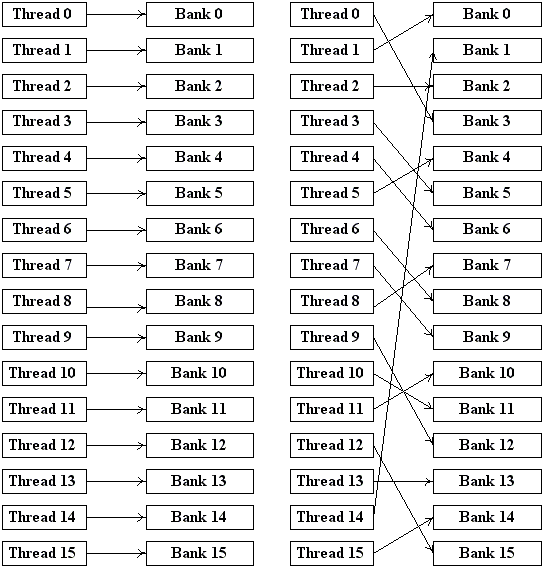
Рис 4. Паттерны безконфликтного доступа к банкам shared-памяти.
Возможен на самом деле еще один случай, когда конфликта банков не происходит - если все нити обращаются к одному и тому же адресу в памяти - в этом случае происходит всего одно обращение к памяти.
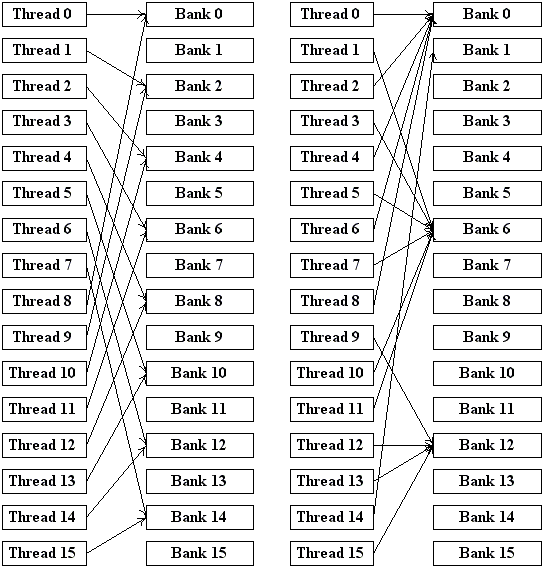
Рис 5. Паттерны доступа, приводящие к конфликтам.
На рис. 5 приведены два способа обращения к shared-памяти, приводящие к возникновению конфликтов.
Довольно часто используемым приемом при работе с shared-памятью является загрузка блока большой исходной матрицы в небольшую (обычно 16*16) матрицу в shared-памяти и проведение расчетов используя загруженную матрицу. Именно такой прием был использован в предыдущей статье при умножение матриц.
При этом сама загрузка (когда каждая нить загружает по одному элементу) обычно приводит к объединению запросов в глобальную память. Однако при обработке полученной небольшой матрицы в shared-памяти следует иметь в виду, что если ее размер кратен 16, то каждый ее столбец размещается с одном банке. Поэтому если каждая нить по очереди перебирает элементы сперва из первого столбца, затем из второго и т.д., то мы сразу получаем конфликт банков, причем порядка 16.
Самым простым способом избежать этого является дополнение матрицы еще один столбцом (т.е. от матрицы из 16 столбцов мы переходим к матрице из 17 столбцов). За счет этого расположение столбцов в памяти сдвигается и каждый столбец теперь равномерно распределяется по всем банкам памяти.
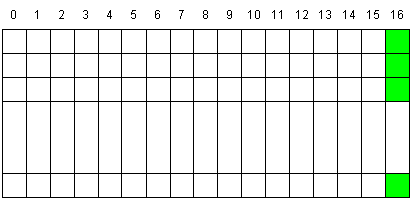
Рис 6. Дополнение матрицы.
Вообще подобный прием - добавление к каждой строке матрицы нескольких дополнительных байт довольно распространен в CUDA - за счет его при доступе к глобальной памяти мы легко гарантируем выравнивание для начала строки, а при доступе к shared-памяти - равномерное распределение столбца по банкам памяти.
Когда нитям блока не хватает имеющихся на мультипроцессоре регистров, то для размещения локальных переменных используется локальная память GPU. Локальная память размещена в DRAM и не кэшируется, поэтому доступ к ней такой же медленный как и к глобальной памяти. Однако компилятор обеспечивает, что запросы отдельный нитей к локальной памяти объединяются в одну транзакцию (coalescing).
Для оптимизации программ на CUDA важно точно знать сколько времени (тактов, clocks) занимает выполнение той или иной команды.
Выполнение следующий действий требует 4 тактов мультипроцессора:
Функции 1/x, 1/sqrt(x) и __logf(x) выполняются за 16 тактов.
Целочисленное умножение (32-битовое) также требует 16 тактов, однако во многих случаях вместо него можно воспользоваться функциями __mul24(x,y) и __umul24(x,y), которые занимают всего 4 такта, но осуществляют 24-битовое умножение (т.е. если числа не очень большие - старший байт равен нулю - то эти функции точно заменяют умножение).
Крайне дорогостоящими операциями, которые желательно избегать, оказывается целочисленное деление (x/y) и целочисленный остаток от деления (x%y). В ряде случае их можно заменять побитовыми операциями, в случае когда идет деление на константу (являющуюся степенью двух) или взятие остатка от деления на константу (вида 2^n-1 ), то компилятор сам заменяет операцию на побитовую.
Квадратный корень реализуется как суперпозиция двух операций 1/x и 1/sqrt(x) и поэтому занимает 32 такта.
Деление на значение типа float требует 36 тактов, однако есть функция __fdividef(x,y), осуществляющая деление за 20 тактов (но возвращающая ноль при очень больших значениях y).
Функции __sinf(x), __cosf(x) и __expf(x) требуют 32 тактов, функции sinf(x), cosf(x), sincos(x) и tanf(x) гораздо более дорогостоящи, особенно для x>48039.
Кроме того компилятор может вставлять команды для приведения типа в следующих случаях:
Поэтому рекомендуется явно указывать тип float, например вместо 1.3 писать 1.3f и использовать float-аналоги функций (например __sinf или sinf вместо sin).
Обращение к памяти занимает 4 такта, при обращении к глобальной памяти следует также добавить еще от 400 до 600 тактов.
Вызов __syncthreads() требует 4 тактов, если не нужно ждать ни одной нити в warp'е.
Одной из часто встречающихся задач являются так называемая редукция массив (reduction). Пусть у нас есть массив a0,a1,...,aN-1 и некоторая бинарная операция или функция (например сложение).
Тогда следующее выражение будет называться редукцией массива a0,a1,...,aN-1 относительно заданной операции (в нашем случае сложения):
A=((a0+a1)+...+aN-1
В качестве бинарной операции также может выступать умножение, минимум млм максимум, давая в результате произведение всех элементов массива или минимальный/максимальный элемент массива. Точно также скалярное произведение двух больших массивов является редукцией поэлементного произведения этих массивов.
На примере реализации редукции в CUDA мы рассмотрим основные элементы оптимизации программы.
Обратите внимание на то, что в CUDA есть ограничение - количество блоков по каждому измерению (т.е. размер grid'а по каждому измерению не может превышать 65535). В нашем случае, поскольку мы работаем с одномерным массивом и одномерный grid является наиболее подходящим способом организации блоков, это накладывает ограничения на размер входного массива. Однако данное ограничение не принципиально - можно легко переписать рассматриваемые ниже варианты для двух- или трехмерных grid'ов.
Первое с чем нужно определиться - это что является лимитирующим быстродействие фактором - арифметические операции или доступ к памяти. В нашем случае очевидно, что лимитировать нас будет именно доступ к памяти и именно этот доступ и нужно оптимизировать в первую очередь.
Первый шаг довольно прост - каждому блоку соответствует часть массива (делим массив поровну между всеми блоками). Задача блока найти сумму всех элементов своей части и записать результирующее значение в выходной массив. При этом каждой нити соответствует по одному элементу массива, сначала каждая нить загружает свой элемент в shared-память, а затем иерархически суммирует, как показано на рис 6.
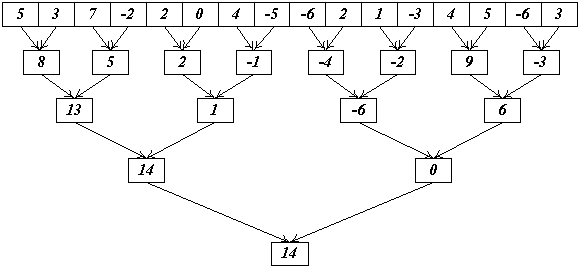
Рис 6. Иерархическое суммирование элементов внутри блока.
Далее мы рассмотрим именно оптимизацию этого шага - нахождение каждым блоком своей суммы наиболее эффективным образом. Будем использовать одномерный массив блоков, где каждый блок является одномерным массивом нитей. Ниже приводится ядро, осуществляющего параллельную редукцию описанным методом:
__global__ void reduce1 ( int * inData, int * outData )
{
__shared__ int data [BLOCK_SIZE];
int tid = threadIdx.x;
int i = blockIdx.x * blockDim.x + threadIdx.x;
data [tid] = inData [i]; // load into shared memeory
__syncthreads ();
for ( int s = 1; s < blockDim.x; s *= 2 )
{
if ( tid % (2*s) == 0 )
data [tid] += data [tid + s];
__syncthreads ();
}
if ( tid == 0 ) // write result of block reduction
outData [blockIdx.x] = data [0];
}
На следующем рисунке проиллюстрирована схема работы данного подхода.
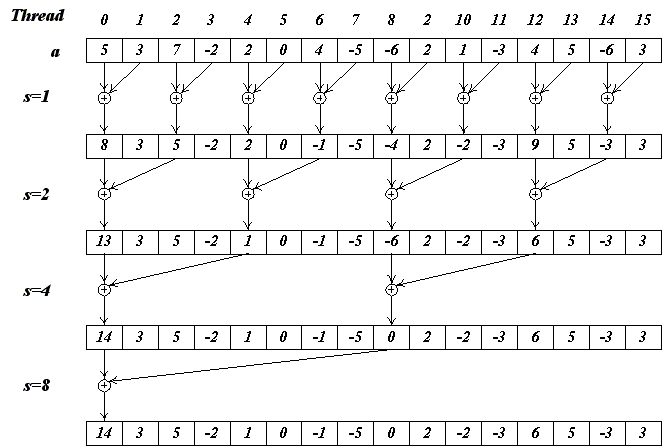
Рис 7.
Сразу виден большой недостаток этого подхода - условный оператор приводит к сильному ветвлению кода внутри каждого warp'а. Его можно избежать переписав ядро следующим образом:
__global__ void reduce1 ( int * inData, int * outData )
{
__shared__ int data [BLOCK_SIZE];
int tid = threadIdx.x;
int i = blockIdx.x * blockDim.x + threadIdx.x;
data [tid] = inData [i]; // load into shared memeory
__syncthreads ();
for ( int s = 1; s < blockDim.x; s <<= 1 )
{
int index = 2 * s * tid;
if ( index < blockDim.x )
data [index] += data [index + s];
__syncthreads ();
}
if ( tid == 0 ) // write result of block reduction
outData [blockIdx.x] = data [0];
}
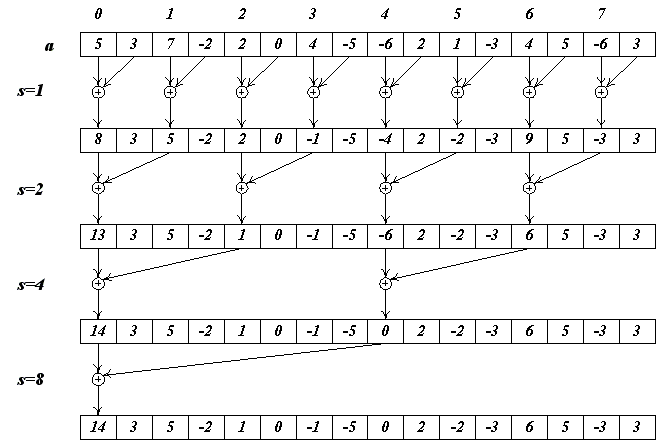
Рис 8.
Как видно из рисунка, получается почти такая же схема, но распределение операций и элементов по нитям изменилось, за счет чего и удалось получить минимальное ветвление.
Однако данный подход имеет серьезный недостаток - он приводит в большому числу конфликтов банков при обращении к shared-памяти - так при s>1 у нас не будет ни одного обращения к банкам с нечетными номерами, а на банки с четными номерами придется двойная нагрузка. По мере увеличения s количество неиспользуемых банков (а, значит, и нагрузка на остальные) будет только расти..
Для того, чтобы избежать подобной проблемы реорганизуем саму схему суммирования - начнем суммировать не с соседних элементов, а наоборот - с элементов, удаленных друг от друга на dimBlock.x/2. На следующем шаге будем суммировать элементы, удаленные друг от друга на dimBlock.x/2 и т.д. (см. рис 9).
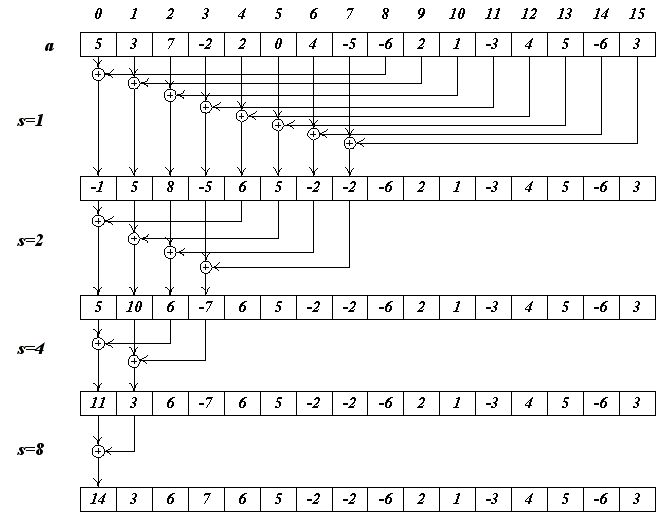
Рис 9.
Соответствующая схема реализуется следующим ядром:
__global__ void reduce3 ( int * inData, int * outData )
{
__shared__ int data [BLOCK_SIZE];
int tid = threadIdx.x;
int i = blockIdx.x * blockDim.x + threadIdx.x;
data [tid] = inData [i]; // load into shared memeory
__syncthreads ();
for ( int s = blockDim.x / 2; s > 0; s >>= 1 )
{
if ( tid < s )
data [index] += data [index + s];
__syncthreads ();
}
if ( tid == 0 ) // write result of block reduction
outData [blockIdx.x] = data [0];
}
Хотя мы заметно сократили число конфликтов банков в shared-памяти, но в результате получили что на первой итерации цикла по s половина всех нитей простаивает.
Хотя с точки зрения ветвления в этом никаких проблем нет (при большом размере блока, кратном 64, у нас все простаивающие нити будут собраны в warp'ы), но все равно имеется неэффективность, которую хочется удалить.
Хочется, чтобы уже на первой итерации цикла все нити были загружены. Для этого необходимо уменьшить вдвое количество блоков, но при этом каждому блоку выделить вдвое больше слов. При этом самое первое суммирование может быть выполнено сразу же при загрузке данных в shared-память (т.е. мы не увеличиваем требуемый объем shared-памяти).
__global__ void reduce4 ( int * inData, int * outData )
{
__shared__ int data [BLOCK_SIZE];
int tid = threadIdx.x;
int i = 2 * blockIdx.x * blockDim.x + threadIdx.x;
data [tid] = inData [i] + inData [i+blockDim.x]; // load into shared memeory
__syncthreads ();
for ( int s = blockDim.x / 2; s > 0; s >>= 1 )
{
if ( tid < s )
data [tid] += data [tid + s];
__syncthreads ();
}
if ( tid == 0 ) // write result of block reduction
outData [blockIdx.x] = data [0];
}
int main ( int argc, char * argv [] )
{
int numBytes = N * sizeof ( int );
int n = N;
int i = 0;
int sum = 0;
// allocate host memory
int * a = new int [N];
int * b = new int [N];
// init with random values
for ( i = 0; i < N; i++ )
{
a [i] = 1; //(rand () & 0xFF) - 127;
sum += a [i];
}
// allocate device memory
int * adev [2] = { NULL, NULL };
cudaEvent_t start, stop;
float gpuTime = 0.0f;
cudaMalloc ( (void**)&adev [0], numBytes );
cudaMalloc ( (void**)&adev [1], numBytes );
// create cuda event handles
cudaEventCreate ( &start );
cudaEventCreate ( &stop );
// asynchronously issue work to the GPU (all to stream 0)
cudaEventRecord ( start, 0 );
cudaMemcpy ( adev [0], a, numBytes, cudaMemcpyHostToDevice );
for ( i = 0; n >= BLOCK_SIZE; n /= (2*BLOCK_SIZE), i ^= 1 )
{
// set kernel launch configuration
dim3 dimBlock ( BLOCK_SIZE, 1, 1 );
dim3 dimGrid ( n / (2*dimBlock.x), 1, 1 );
reduce4<<<dimGrid, dimBlock>>> ( adev [i], adev [i^1] );
}
cudaMemcpy ( b, adev [i], 4*N, cudaMemcpyDeviceToHost );
cudaEventRecord ( stop, 0 );
cudaEventSynchronize ( stop );
cudaEventElapsedTime ( &gpuTime, start, stop );
for ( i = 1; i < n; i++ )
b [0] += b [i];
// print the cpu and gpu times
printf ( "time spent executing by the GPU: %.2f milliseconds\n", gpuTime );
printf ( "CPU sum %d, CUDA sum %d, N = %d\n", sum, b [0], N );
// release resources
cudaEventDestroy ( start );
cudaEventDestroy ( stop );
cudaFree ( adev [0] );
cudaFree ( adev [1] );
delete a;
delete b;
return 0;
}
В качестве заключительной оптимизации заметим, что при s<=32 у нас в каждом блоке останется всего по одному warp'у, поэтому синхронизация уже не нужна и проверка tid<s также не нужна (она все равно ничего в этом случае не делает). Поэтому развернем цикл для s<=32:
__global__ void reduce5 ( int * inData, int * outData )
{
__shared__ int data [BLOCK_SIZE];
int tid = threadIdx.x;
int i = 2 * blockIdx.x * blockDim.x + threadIdx.x;
data [tid] = inData [i] + inData [i+blockDim.x]; // load into shared memeory
__syncthreads ();
for ( int s = blockDim.x / 2; s > 32; s >>= 1 )
{
if ( tid < s )
data [tid] += data [tid + s];
__syncthreads ();
}
if ( tid < 32 ) // unroll last iterations
{
data [tid] += data [tid + 32];
data [tid] += data [tid + 16];
data [tid] += data [tid + 8];
data [tid] += data [tid + 4];
data [tid] += data [tid + 2];
data [tid] += data [tid + 1];
}
if ( tid == 0 ) // write result of block reduction
outData [blockIdx.x] = data [0];
}
В результате выполнения такого ядра над входным массивом, в выходном массиве для каждого блока появится сумма всех элементов данного блока. Тем самым мы получили новый массив, который также следует суммировать аналогичным способом, до тем пор, пока мы не получим окончательный массив размера, меньшего чем dimBlock.x. Элементы этого массива можно просуммировать уже на CPU.
В следующей таблице приведены быстродейстия для всех рассмотренных подходов.
| Вариант алгоритма | Время выполнения (в миллисекундах) |
|---|---|
| reduce1 | 19.09 |
| reduce2 | 11.91 |
| reduce3 | 10.62 |
| reduce4 | 9.10 |
| reduce5 | 8.67 |