

|
Главная
 Статьи
Статьи
 Ссылки
Ссылки
 Скачать
Скачать
 Скриншоты
Скриншоты
 Юмор
Юмор
 Почитать
Почитать
 Tools
Tools
 Проекты
Проекты
 Обо мне
Обо мне
 Гостевая
Гостевая


|
Одним из простейших (и до сих пор активно используемых) способов анимации мешей (обычно игровых персонажей) является т.н. анимация основанная на ключевых кадрах (keyframe animation).
Она заключается в том, что для каждой вершины мэша хранятся ее координаты для некоторого набора моментов времени (ключевых кадров, key frames) t0,t1,...,tn.
vi,j=vi(tj),j=1,...,n
Тогда, если нам требуется получить координаты вершины в некоторый момент времени t, то просто ищется пара соседних ключевых кадров ti<=t<=ti+1. После этого просто путем линейной интерполяции между координатами точки в этих кадрах находятся требуемые координаты вершины в момент времени t.
Хотя такой способ крайне прост и дешев в плане вычислений, он обладает и целым рядом недостатков. Наиболее серьезными, IMHO, является необходимость хранения очень большого набора данных (координаты каждой вершины для каждого ключевого кадра) и очень большая сложность учета физики, изменения анимации налету (например, учитывание толчка от попадания пули в плечо противнику или падение тела с лестницы).
Для повышения гибкости часто идут путем разбиения всей модели (меша) на несколько отдельных подмешей, каждый со своим набором анимаций, и соединенных между собой при помощи афинного преобразования координат.
Именно этот подход был использован в игре Quake III Arena, где каждая модель игрока состояла из трех отдельных частей (каждая из этих частей задавалась отдельным md3-файлом). Оружие игрока выступало как еще один отдельный меш. При этом все эти меши были объединены в иерархическую структуру и связаны между собой преобразованиями поворота и переноса.
Такой подход хотя и повышает гибкость, но в целом проблемы так и не решает.
И тут на помощь приходит очень красивый и простой способ называемый скелетной анимацией (skeletal animation).
Основная идея скелетной анимации заключается в задании некоторого (иерархически организованного ) скелета, относительно которого и задаются все вершины модели. При этом размер самого скелета (количество костей в нем) очень мало (по сравнению с числом вершин меша).
Тогда достаточно просто анимировать данный скелет (в том числе и с учетом физики), а по полученному скелету находить (на CPU или GPU) новые координаты всех вершин.
Обратите внимание, что именно скелет отвечает за динамику модели и одному скелету может соответствовать несколько различных моделей.
Мы по-прежнему можем применять keyframe animation, но только уже по отношению к скелету, а это требует хранения гораздо меньшего объема данных.
Скелет в простейшем случае представляет из себя набор костей (bones, joints), соединенных иерархическим образом. На рис. 1 приведены скелеты нескольких персонажей из игры DooM III.
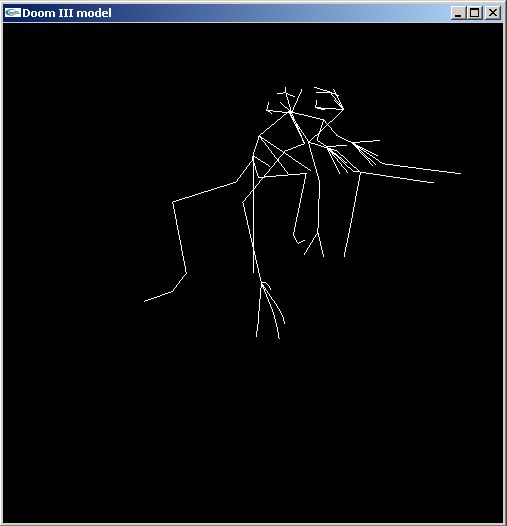
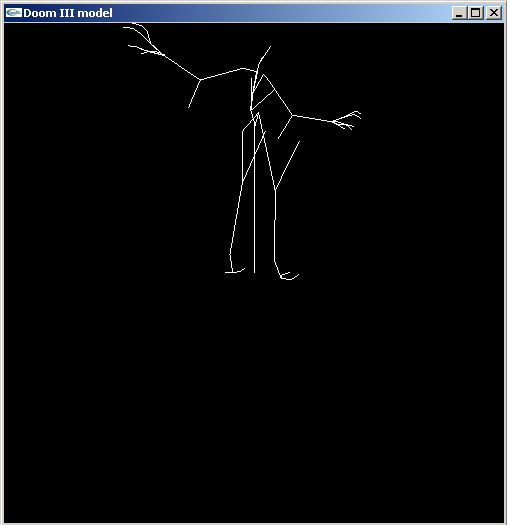
Рис 1. Скелеты моделей из игры DooM III.
Каждая кость скелета - это отрезок, начало которого подсоединено к концу "родительской кости" (parent bone).
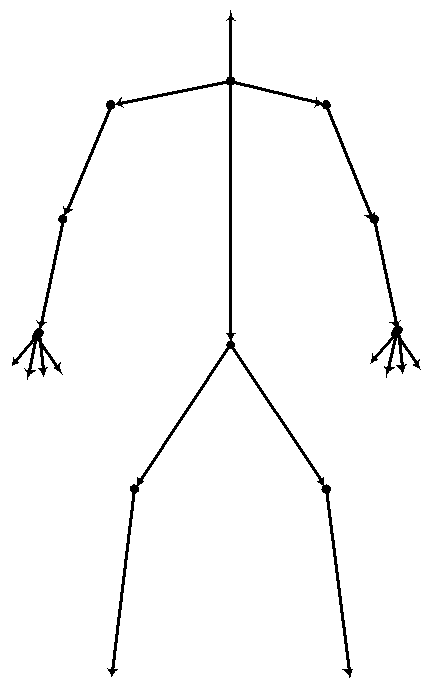
Рис 2. Пример простого скелета для модели человека.
Поскольку начало кости полностью задается родительской костью, то для однозначного задания кости необходимо задать ссылку на родительскую кость и конец отрезка.
Конец отрезка обычно задается как афинное преобразование не изменяющее длины (изометризм), переводящее начало кости в ее конец.
Можно показать, что такое преобразование всегда представляет из себя суперпозицию поворота и переноса.
Самым удобным способом задания поворота является использование единичных кватернионов.
Тем самым мы приходим к следующей структуре данных для представления кости скелета:
struct Bone
{
Bone * parent;
Quaternion orient;
Vector3D pos;
};
При этом каждая кость, кроме корневой (root'а:))) имеет родителя, в системе координат которого он и задает свой конец (см. рис. 3).
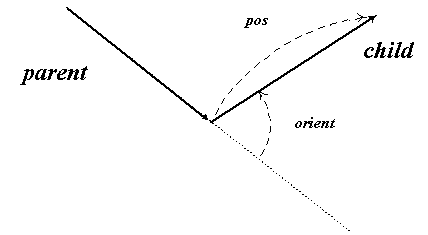
Рис 3. Кость и ее родительская кость.
Обычно весь скелет задается как массив костей упорядоченных таким образом, что для любой кости ее родительская кость идет в массиве раньше ее самой. Тогда кость с нулевым индексом является корневой. В этом случае можно ссылку на родительскую кость просто заменить ее индексом в этом массиве.
Удобно с каждой костью сразу же связать и соответствующее афинное преобразование (а также и обратное преобразование), задаваемое ею:
struct Bone
{
Bone * parent;
Quaternion orient;
Vector3D pos;
Vector3D transform ( const Vector3D& v ) const
{
return orient.rotate ( v ) + pos;
}
Vector3D invTransform ( const Vector3D& v ) const
{
Quaternion c ( orient );
return c.conj ().rotate ( v - pos );
}
};
В описанной выше схеме поворот и перенос для каждой кости задаются относительно конца ее родительской кости. Однако в целом ряде случаев (например при построении вершин анимируемой модели) нам нужно знать преобразование, задаваемое костью относительно системы координат модели, т.е. корня скелета.
Рассмотрим простейший случай скелета из двух костей - b0 и b1 (см. рис. 4).
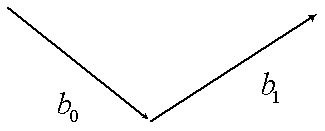
Рис 4. Скелет из двух костей.
Пусть кости bi соответствует поворот, задаваемый кватернионом qi, и перенос, задаваемый вектором pi.
Для кости b0 параметры q0 и p0 задают ее преобразование относительно глобальной (по отношению ко всей модели) системы координат.
Однако уже для кости b1 все обстоит сложнее - задаваемое ей преобразование является на самом деле суперпозицией двух преобразований - ее собственного (q1, p1) и преобразования родительской кости (q0, p0).
Легко убедиться что преобразование, задаваемое костью b1 относительно глобальной системы координат (q1*, p1*) задается следующими формулами:
q1* = q0*q1,
p1* = p0+q0(p1)
Тем самым с каждой костью можно связать два преобразования - одно относительно родительской кости, а другое - относительно глобальной системы координат, последнее преобразование иногда называется абсолютным.
При построении вершин по скелету гораздо удобнее пользоваться абсолютными преобразованиями для каждой кости скелета, а вот для задания анимации (как основанной на ключевых кадрах, так и физической) гораздо удобнее использовать относительные преобразования - они позволяют рассматривая одну кость не думать о всех остальных костях.
Поскольку при анимации связность костей (т.е. структура скелета - отношение child-parent между костями) не изменяется, то при использовании ключевых кадров для скелетной анимации достаточно для каждой кости скелета для каждого ключевого кадра задать всего шесть чисел - три задают перенос и еще три служат для задания поворота (единичный кватернион определяется всего тремя своими координатами, четвертая легко находится по первым трем).
Поскольку количество костей (по сравнению с количеством вершин модели) заметно меньше, то мы получаем выигрыш в объеме данных, требуемых для хранения анимации. Кроме того, за счет использования т.н. сферической линейной интерполяции кватернионов (slerp) можно получить более реалистически выглядящее движение на меньшем количестве ключевых кадров.
Рассмотрим теперь как можно при помощи скелета задавать вершины модели.
Простейшим случаем является сопоставление каждой вершине определенной кости, относительно конца которой и задается вершина (рис 5.)
Рис 5. Задание вершин относительно заданной кости.
Тогда для нахождения положения вершины по заданному скелету нам достаочно лишь найти абсолютное преобразование, задаваемое требуемой костью и преобразовать при помощи его координаты вершины.
Как известно, если преобразование для вершин задается при помощи однородной матрицы M (размера 4х4), то нормали (и другие вектора, "прикрепленные" к модели) преобразуются при помощи обращенной и транспонированной верхней левой 3х3 подматрицы матрицы M.
Однако в случае скелетной анимации применяемые преобразования представляют собой композицию поворота и переноса (причем за перенос отвечает крайний правый столбец матрицы M), то верхняя левая 3х3 подматрица - это матрица поворота.
Однако для любой матрицы поворота R (так как она является ортогональной матрицей) справедливо следующее равенство R-1=RT. Поэтому вектор нормали (а также касательный вектор и бинормаль) преобразуются поворотом при помощи кватерниона, задающего поворот.
Поэтому когда необходимо найти не только положение вершины, но и связанные с мэшем направления (нормаль, касательный вектор, и т.д.), то строится абсолютное преобразование для кости, состоящее из поворота и переноса.
Сама вершина преобразуется с использованием как поворота, так и переноса, а вектора направлений преобразуются только при помощи поворота.
В игре DooM III использовалась более гибкая схема - для каждой вершины задается не одна кость, а несколько. Для каждой из таких костей кроме положения вершины относительно нее задается также и вклад данной кости (ее вес). Результирующее положение вершины берется как взвешенная сумма преобразованных костями вершин (в качестве веса используется вес, приписываемый данной кости для данной вершины). Для любой вершины сумма всех весов должна равняться единице.
Это позволяет при анимации вершины учитывать сразу несколько костей, что позволяет создавать более реалистичную анимацию.
В случае использования сразу нескольких костей для задания положения вершины, нормаль и другие вектора также строятся с использованием нескольких костей. Сперва нормаль поворачивается при помощи абсолютного преобразование поворота, задаваемого костью, затем получившиеся вектора складываются с учетом весов, после чего полученный результат нормируется (хотя поворот и не изменяет длины вектора, но вот сумма единичных векторов скорее всего уже не будет единичным вектором).
Таким образом все анимации (в том числе и получаемая путем физических расчетов для скелета) персонажа сводятся к анимации самого скелета.
После того, как для заданного момента времени, скелет найден, то сперва для каждой кости находится абсолютное преобразование, задаваемое ею, а потом вычисляются положения всех вершин модели и производится рендеринг.
Далее мы рассмотрим скелетную анимацию на примере моделей из игры Doom III. Большим удобством такого выбора является не только достаточно гибкая схема анимации, но также и тот факт, что все данные игры хранятся в обычных zip-файлах, причем описания моделей и анимаций задаются обычными текстовыми файлами с довольно простой структурой.
Для задания самой модели используются файлы с расширением .md5-mesh, а для задания анимации для модели используются файлы с расширением .md5-anim.
Файл с расширением .md5mesh (например, maggot3.md5-mesh) - это обычный текстовый файл, в самом начале которого идут следующие строки:
MD5Version 10 commandline "......" numJoints nnnnn numMeshes mmmmm
Строка, начинающаяся с numJoints, задает количество костей (joints) в скелете модели.
Строка numMeshes задает количество мэшей, из которых состоит заданная модель. Наличие нескольких мэшей в одной модели объясняется тем, что материалы нельзя задавать отдельно для каждого треугольника, а только для набора треугольников. Поэтому вся модель разбивается на несколько мэшей, где каждому мэшу соответствует свой материал, но при этом все мэши строятся на основе одного скелета.
Далее в файле идет группа строк, задающая скелет (обратите внимание, что в данном скелете все преобразования являются абсолютными).
joints {
"name" parent ( pos.x pos.y pos.z ) ( orient.x orient.y orient.z )
. . .
}
Каждая строка, заключенная между строками "joints {" и "}", несет информацию об одной кости скелета (полное количество костей задается строкой numJoints).
Описание каждой кости начинается с ее имени (в кавычках), далее идет индекс родительской кости ( или -1 для корня), координаты конца и ориентация кости (относительно глобальной системы координат).
При этом для кватерниона задается лишь первые три его компоненты, четвертая находится из условия нормировки при помощи следующей функции:
void renormalize ( Quaternion& q )
{
double len = 1 - q.x*q.x - q.y*q.y - q.z*q.z;
if ( len < EPS )
q.w = 0;
else
q.w = -sqrt ( len );
}
После описания скелета идут описания мэшей. Каждое такое описание имеет следующий вид:
mesh {
shader "shader-name"
numverts nnnn
vert vertIndex ( s t ) startWeight numWeights
vert . . .
. . .
numtris mmm
tri triIndex vertIndex [0] vertIndex [1] vertIndex [2]
tri . . .
numweights kkkk
weight weightIndex joint bias ( pos.x pos.y pos.z )
weight . . .
. . .
}
Строка shader задает имя файла (с расширением mtr), описывающего материал (шейдер), который следует использовать для рендеринга данного мэша.
Строка numverts задает количество вершин для данного мэша. После нее идут строки (начинающиеся с vert) - по одной на каждую вершину.
Описание вершины состоит из следующих параметров - ее номера (vertIndex), текстурных координат s и t, номера первого веса (startWeight) и количества подряд идущих весов, используемых для вычисления координат данной вершины (numWeights).
После описания всех вершин идет описание всех треугольников, составляющих данный мэш.
Описания треугольников начинаются со строки numtris, задающей общее количество треугольников в данном мэше. После нее идет по одной строке (начинающейся с tri) на каждый треугольник.
Для каждого треугольника задается его номер (triIndex) и индексы (в массив вершин) трех образующих его вершин (vertIndex []).
После задания всех треугольников идет задание весов.
Фактически вес (weight) - это координаты вершины относительно одной кости вместе с весовым коэффициентом, определяющим вклад данной кости в итоговые координаты точки.
Как уже отмечалось, каждый вес - это координаты какой-либо вершины относительно одной из костей, вместе с вкладом этих координат в итоговые координаты вершины.
При этом массив весов упорядочен по вершинах - все веса, соответствующие одной вершине идут подряд.
Вначале строка numweights задает общее количество весов для данного мэша. После нее идут строки (начинающиеся с weight), задающие отдельные веса.
Описание каждого веса состоит из его номера (weightIndex), номера кости (joint), относительно которой задаются координаты, вклада данного веса (bias) и собственно самих координат вершины относительно данной кости (pos).
Для облегчения работы с моделями из Doom III введем несколько простых классов (полный исходный код для всех примеров можно скачать со ссылке в конце статьи).
struct Vertex // mesh vertex
{
Vector2D tex;
int weightIndex;
int weightCount;
};
struct Triangle
{
int index [3];
};
struct Weight
{
int jointIndex; // for whuch bone this weight is for
float weight; // looks like a weight of this pos
Vector3D pos;
};
class BaseFrameJoint
{
public:
Vector3D pos;
Quaternion orient;
};
class Joint
{
public:
string name;
int parentIndex;
Joint * parent;
Vector3D pos;
Quaternion orient;
Vector3D transform ( const Vector3D& v ) const
{
return orient.rotate ( v ) + pos;
}
Vector3D invTransform ( const Vector3D& v ) const
{
Quaternion c ( orient );
return c.conj ().rotate ( v - pos );
}
};
Также нам понадобятся классы для представления отдельных мэшей и всей модели целиком. Описание этих классов приводится ниже.
class Md5Mesh
{
public:
string shader;
int numVertices;
Vertex * vertices;
int numTris;
Triangle * tris;
int numWeights;
Weight * weights;
Vector3D * points;
unsigned diffuseMap;
unsigned specularMap;
unsigned bumpMap;
public:
Md5Mesh ();
~Md5Mesh ();
void setNumVertices ( int n );
void setNumTris ( int n );
void setNumWeights ( int n );
void setShader ( const string& sh )
{
shader = sh;
}
void setVertex ( int index, const Vector2D& tex, int blendIndex, int blendCount );
void setTri ( int index, int i1, int i2, int i3 );
void setWeight ( int index, int bone, float bias, const Vector3D& weight );
void calcPoints ( Joint * joints ); // compute real points from bones data
void draw (); // draw itself
bool loadShader ( const string& path ); // load textures
friend class Model;
};
class Md5Model
{
public:
int numJoints;
Joint * joints;
int numMeshes;
Md5Mesh * meshes;
public:
Md5Model ();
~Md5Model ();
int getNumJoints () const
{
return numJoints;
}
Joint * getJoints () const
{
return joints;
}
void setNumJoints ( int n );
void setNumMeshes ( int n );
bool load ( const string& modelName );
bool loadJoints ( Data * data );
void compute ( Joint * joints );
void draw ();
void drawSkeleton ( bool absoluteJoints, Joint * joints );
protected:
void drawJoint ( Joint * joints, int i1, int i2, bool absoluteJoints );
};
Наиболее интересными методами класса Md5Mesh являются методы calcPoints и draw.
Первый из них вычисляет координаты всех вершин по заданному скелету, а второй метод строит строит изображение данного мэша по набору ранее вычисленных вершин.
Ниже приводятся реализации этих методов.
void Md5Mesh :: calcPoints ( Joint * joints ) // compute real points from bones data
{
for ( int i = 0; i < numVertices; i++ )
{
Vertex& v = vertices [i]; // current vertex
Vector3D p ( 0, 0, 0 );
for ( int k = 0; k < v.weightCount; k++ )
{
Weight& weight = weights [v.weightIndex + k];
Joint& joint = joints [weight.jointIndex];
// transform weight.pos by bone with weight
p += joint.transform ( weight.pos ) * weight.weight;
}
points [i] = Vector3D ( p.y, p.x, p.z );
}
}
void Md5Mesh :: draw () // draw itself
{
glBindTexture ( GL_TEXTURE_2D, diffuseMap );
glBegin ( GL_TRIANGLES );
for ( int i = 0; i < numTris; i++ )
{
for ( int k = 0; k < 3; k++ )
{
int index = tris [i].index [k];
glTexCoord2fv ( vertices [index].tex );
glVertex3fv ( points [index] );
}
}
glEnd ();
}
Ниже приводятся исходный текст методов класса Md5Model, связанных с расчетом вершин и рисованием.
При этом есть как метод, позволяющий построить только скелет (drawSkeleton), так и метод, строящий нормальное изображение всей модели (draw).
void Md5Model :: compute ( Joint * joints )
{
for ( int i = 0; i < numMeshes; i++ )
meshes [i].calcPoints ( joints );
}
void Md5Model :: draw ()
{
for ( int i = 0; i < numMeshes; i++ )
meshes [i].draw ();
}
void Md5Model :: drawSkeleton ( bool absoluteJoints, Joint * joints )
{
glDisable ( GL_DEPTH_TEST );
glDisable ( GL_TEXTURE_2D );
glColor3f ( 1, 1, 1 );
for ( int i = 1; i < numJoints; i++ )
drawJoint ( joints, i, joints [i].parentIndex, absoluteJoints );
glEnable ( GL_TEXTURE_2D );
glEnable ( GL_DEPTH_TEST );
}
void Md5Model :: drawJoint ( Joint * j, int i1, int i2, bool absoluteJoints )
{
if ( i1 < 0 || i2 < 0 )
return;
Vector3D p1 ( j [i1].pos );
Vector3D p2 ( j [i2].pos );
if ( !absoluteJoints )
{
for ( int i = j [i1].parentIndex; i >= 0; i = j [i].parentIndex )
p1 += j [i].pos;
for ( i = j [i2].parentIndex; i >= 0; i = j [i].parentIndex )
p2 += j [i].pos;
}
glBegin ( GL_LINES );
glVertex3f ( p1.y, p1.x, p1.z );
glVertex3f ( p2.y, p2.x, p2.z );
glEnd ();
}
Для хранения анимаций для персонажей в DooM III используются файлы с расширением .md5anim. При этом на один .md5mesh-файла часто приходится несколько .md5anim-файлов, содержащих различные варианты анимации (несколько разных способов нападения, движения и т.п.)
Как и .md5mesh-файлы файлы с расширением .md5anim являются обычными текстовыми файлами со похожей структурой.
Каждый такой файл начинается со следующих строк:
MD5Version 10 commandline "......" numFrames nnn numJoints mmm frameRate kkk numAnimComponents lll
Параметр numFrames задает общее количество ключевых кадров для данной анимации. Следующий параметр - numJoints задает количество костей в скелете, он должен совпадать с соответствующим параметром в .md5mesh-файле.
Параметр frameRate задает скорость анимации в ключевых кадрах в секунду.
Параметр numAnimComponents задает количество параметров на кадр, используемых для анимации.
После этих строк (заголовка) идет блок строк, задающих иерархическую структуру скелета. Этот блок имеет следующий вид:
hierarchy {
"name" parent flags startIndex
. . .
}
Для каждой кости задается ее имя, индекс родительской кости (parent), флаги (flags), определяющие какие параметры данной кости будут изменяться в ходе анимации, и индекс в массив значений (startIndex), начиная с которого следует брать значения для анимируемых компонент.
После блока, задающего иерархию, следует блок, задающий AABB для каждого кадра и имеющий следующий вид:
bounds {
( min.x min.y min.z ) ( max.x max.y max.z )
. . .
}
За этим блоком идет блок, задающие преобразования для каждой из костей скелета относительно родительской кости. Этот блок имеет следующую структуру:
baseframe {
( pos.x pos.y pos.z ) ( orient.x orient.y orient.z )
. . .
}
Как и ранее, первые три параметра задают перенос, а следующие три - первые три компоненты единичного кватерниона, определяющего поворот.
Сразу же за этим блоком идут наборы вещественных чисел для каждого кадра анимации. При анимации скелета именно из этого массива (для требуемого кадра) и берутся новые значения для параметров костей. Для каждой кости параметр startIndex из блок hierarchy задает место в этом наборе, начиная с которого следует брать числа для анимации данной кости. Этот набор имеет следующий формат:
frame frameIndex {
fff fff fff fff fff ...
. . .
}
Для построения скелета, соответствующего требуемому номеру кадра, берется базовый скелет (baseFrame), после чего для каждой его кости отдельные ее параметры заменяются значениями из массива чисел, задаваемого секцией frame.
Какие именно числа, задающие локальное преобразование кости скелета, следует заменить, определяется битами поля flags.
Если у этого поля выставлен бит 1 (flags & 1 != 0), то величина pos.x заменятся соответствующим значением из массива значений, задаваемого секцией frame.
Если у этого поля выставлен бит 2 (flags & 2 != 0) или 4 (flags & 4 != 0), то величина pos.y или pos.z заменятся соответствующими значениями из массива значений, задаваемого секцией frame.
Биты 8, 16 и 32 задают изменение параметров orient.x, orient.y и orient.z.
Для хранения информации о иерархии и базовом скелете далее мы будем использовать следующие классы:
class HierarchyItem
{
public:
string name;
int parent;
int flags;
int startIndex;
};
class BaseFrameJoint
{
public:
Vector3D pos;
Quaternion orient;
};
Тогда построении скелета по заданному номеру кадра реализуется следующим фрагментом кода:
void setFrame ( int no )
{
if ( no < 0 )
no = numFrames - 1;
if ( no >= numFrames )
no = 0;
frame = no;
resetJoints ();
for ( int i = 0; i < numJoints; i++ )
{
int flags = hierarchy [i].flags;
int pos = hierarchy [i].startIndex;
if ( flags & 1 )
joints [i].pos.x = frames [no][pos++];
if ( flags & 2 )
joints [i].pos.y = frames [no][pos++];
if ( flags & 4 )
joints [i].pos.z = frames [no][pos++];
if ( flags & 8 )
joints [i].orient.x = frames [no][pos++];
if ( flags & 16 )
joints [i].orient.y = frames [no][pos++];
if ( flags & 32 )
joints [i].orient.z = frames [no][pos++];
renormalize ( joints [i].orient );
}
buildJoints ();
}
Функция resetJoints служит для инициализации "рабочего" скелета, т.е. занесении в него значений базового скелета, используемого в качестве основы при анимации.
void resetJoints ()
{
for ( int i = 0; i < numJoints; i++ )
{
joints [i].name = hierarchy [i].name;
joints [i].parentIndex = hierarchy [i].parent;
joints [i].parent = joints [i].parentIndex == -1 ? NULL :
&joints [joints[i].parentIndex];
joints [i].pos = baseFrame [i].pos;
joints [i].orient = baseFrame [i].orient;
}
}
Функция buildJoints служит для перевода преобразований для каждой кости из локальных (т.е. заданных по отношению к родительской кости) в глобальные (т.е. заданные по отношению к системе координат, в которой задана модель).
void buildJoints ()
{
for ( int i = 0; i < numJoints; i++ )
if ( joints [i].parent != NULL )
{
joints [i].pos = joints [i].parent -> pos +
joints [i].parent -> orient.rotate ( joints [i].pos );
joints [i].orient = joints [i].parent -> orient * joints [i].orient;
}
}
Обычно все эти вычисления проводятся на центральном процессоре. Однако ряд вычислений (при определенных ограничениях) можно перенести на GPU.
Проще всего перенести на GPU вычисление координат вершин по уже готовому скелету. При этом сам скелет можно передавать как два uniform массива четырехмерных векторов. Удобно считать, что корню соответствует нулевой индекс в этих массивах.
Один массив будет содержать сами кватернионы (которые содержат четыре компоненты), а во второй удобно разместить и координаты вектора переноса (в xyz-компонентах) и номер родительской кости (в w-компоненте).
Для реализации скелетной анимации требуется для каждой вершины передать (кроме обычной) следующую информацию - номера используемых ею костей, их веса и координаты относительно каждой из этих костей.
Однако это приводит к необходимости наложить довольно жесткие ограничения на максимально возможное количество костей, используемых при анимации одной вершины.
К сожалению в моделях из DooM III многие модели используют семь и более костей (вплоть до 9 костей на вершину). Хотя это можно перенести на GPU это потребует передачи большого количества вершинных атрибутов общего вида (в то время как OpenGL гораздо эффективнее передает с стандартные атрибуты).
Далее мы рассмотрим упрощенный случай, когда для анимации вершины используется не более четырех костей. Это позволит полностью уложится в текстурные координаты для 8 текстурных блоков.
Текстурные координаты для блоков 0, 1 и 2 обычно задействованы для передачи непосредственно самих текстурных координат и двух векторов - касательного и бинормали, требуемых для реализации бампмэппинга.
А в текстурных координатах блока 3 разместим четыре веса костей, значение компоненты равное нулю, обозначает, что для данной вершины используется менее четырех костей.
Сами данные о четырех костях мы разместим в блоках 4-7. При этом в xyz-компонентах мы будем хранить собственно сами координаты относительно кости, а в w-координате - номер соответствующей кости.

Рис 6. Распределение данных по наборами текстурных координат.
Обратите внимание также, что размеры массивов с данными для скелета необходимо явно задать, поэтому удобно просто заранее задать достаточно большое значение.
Ниже приводится текст простого вершинного шейдера на GLSL, осуществляющего вычисление текстурных вершин по четырем костям описанным выше образом.
//
// GLSL vertex shader for skeletal animation
//
#define N 100
#define EPS 0.001
uniform vec4 boneQuat [N];
uniform vec4 bonePos [N];
//
// Quaternion multiplication
//
vec4 quatMul ( in vec4 q1, in vec4 q2 )
{
vec3 im = q1.w * q2.xyz + q1.xyz * q2.w + cross ( q1.xyz, q2.xyz );
vec4 dt = q1 * q2;
float re = dot ( dt, vec4 ( -1.0, -1.0, -1.0, 1.0 ) );
return vec4 ( im, re );
}
//
// vector rotation via quaternion
//
vec4 quatRotate ( in vec3 p, in vec4 q )
{
vec4 temp = quatMul ( q, vec4 ( p, 0.0 ) );
return quatMul ( temp, vec4 ( -q.x, -q.y, -q.z, q.w ) );
}
vec3 boneTransf ( int index, vec3 pos )
{
return bonePos [index].xyz + quatRotate ( pos, boneQuat [index] ).xyz;
}
void main ()
{
vec4 weights = gl_MultiTexCoord3; // weights for 4 bones
vec3 pos = vec3 ( 0.0 );
int index;
if ( weights.x > EPS ) // process 1st bone
{ // get 1st bone index
index = int ( gl_MultiTexCoord4.w );
pos += weights.x * boneTransf ( index, gl_MultiTexCoord4.xyz );
}
if ( weights.y > EPS ) // process 2nd bone
{ // get 2nd bone index
index = int ( gl_MultiTexCoord5.w );
pos += weights.y * boneTransf ( index, gl_MultiTexCoord5.xyz );
}
if ( weights.z > EPS ) // process 3rd bone
{ // get 3rd bone index
index = int ( gl_MultiTexCoord6.w );
pos += weights.z * boneTransf ( index, gl_MultiTexCoord6.xyz );
}
if ( weights.w > EPS ) // process 4th bone
{ // get 4th bone index
index = int ( gl_MultiTexCoord7.w );
pos += weights.w * boneTransf ( index, gl_MultiTexCoord7.xyz );
}
gl_Position = gl_ModelViewProjectionMatrix * vec4 ( pos, 1.0 );
gl_TexCoord [0] = gl_MultiTexCoord0;
}
Можно пойти другим путем - использование подхода render-to-vertex-buffer позволяет перенести все операции скелетной анимации на GPU. При этом все данные представляются как текстуры и используются фрагментные программы для проведения всех вычислений. Правда такой подход потребует нескольких проходов рендеринга для получения значений вершин, после чего данные из текстуры интерпретируются (или копируются) как вершинных массив и осуществляется нормальный рендеринг.
Данная тема подробно рассматривается в статье о рендеринге в вершинный буфер.
Исходный код ко всем примерам можно скачать здесь. Уже откомпилированные программы для M$ Windows и Linux можно скачать здесь и здесь.