Кривая и код Мортона. Space filling curves

Справедливо не совсем очевидное математическое утверждение: единичный квадрат [0,1]² равномощен (т.е. содержит столько же точек) единичному отрезку [0,1].

Важным шагом в доказательстве данного утверждения было открытие в 1890 году Джузеппе Пеано непрерывной кривой (получившей его имя), проходящей через каждую точку единичного квадрата [0,1]². Кривая Пеано строится как предел последовательности ломаных, приведенных на следующем рисунке.

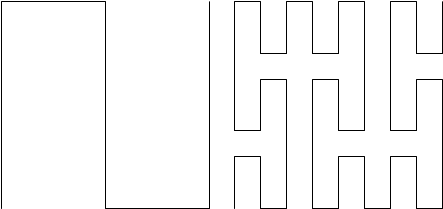
Рис 1. Несколько первых итераций кривой Пеано.

Вслед за Пеано и Давид Гильберт также построил непрерывную кривую, проходящую через каждую точку единичного квадрата. Кривая Гильберта также строится как предел последовательности ломаных, однако использованные им ломаные были заметно проще.

Рис 2. Первые приближения кривой Гильберта.

Можно задать кривую Гильберта при помощи следующей L-системы (в качестве начального состояния выступает строка "L"):

Рис 3. Последовательность итераций кривой Гильберта.

В данной системе через "+" и "-" обозначены повороты налево и направо на 90 градусов, а через "F" - построение отрезка "вперед".

Позже было предложено много подобных кривых, также были построены непрерывные кривые, проходящие через каждую точку единичного N-мерного куба [0,1]^N. Важным свойством таких кривых является то, что каждая из них пересекает себя в любой своей точке. Подобные кривые получили название space-filling curves.

Еще одним примером подобной кривой является кривая Мура, приводимая на следующем рисунке.

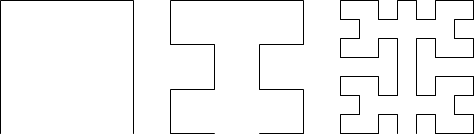
Рис 4. Первые итерации кривой Мура.

Кривую Мура можно задавать при помощи следующей L-системы:

Смысл символов такой же, как и для кривой Гильберта, однако в качестве начальной строки выступает "LFL+F+LFL".

Однако наибольшее практическое применение получила кривая Мортона (или, как ее еще называют, z-кривая). Первые три итерации кривой Мортона приведены на рисунке 5.

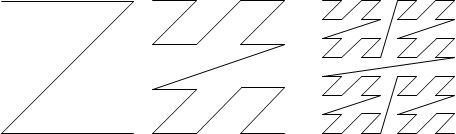
Рис 5. Первые итерации кривой Мортона.

Важным свойством кривой Мортона является то, что если у нас задана решетка 2ⁿx2ⁿ, то можно очень легко построить кривую Мортона, обходящую все узлы этой решетки. Тем самым кривая Мортона позволяет занумеровать узлы этой решетки (номер каждого узла для кривой Мортона называется кодом Мортона этого узла).

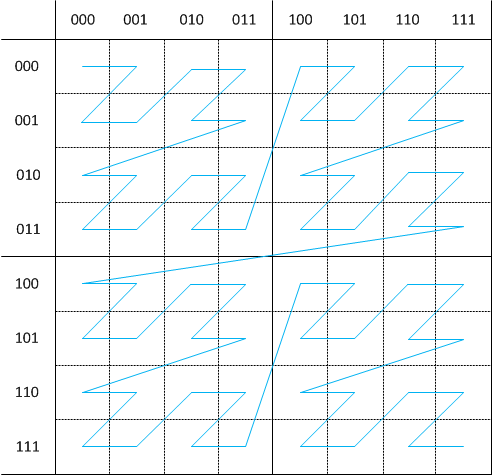
Рис 6. Построение кривой Мортона для решетки 8x8.

Для того, чтобы получить код Мортона для узла (i,j), достаточно просто перевести индексы i и j в бинарное представление (записать в двоичной системе), после чего просто построить новое число, по очереди беря по одному разряду из двоичного представления каждого числа.

Так если у нас есть узел (3,4), то просто берем двоичную запись этих индексов - 011 и 100 и беря по одному разряду из каждого из них получаем двоичную запись кода Мортона для этого узла - 011010. Именно эта простота построения кода Мортона и обеспечила популярность данной кривой.

Для подобного упорядочивания оказывается что понятия "соседства" в смысле положения на кривой (кода Мортона) и соседства в обычном двухмерном пространстве очень близки.

Обратите внимание, что блок исходной решетки размером 2^kx2^k (при условии, что координаты верхнего левого угла кратны 2^k) целиком накрываются одним фрагментов кривой Мортона. Это свойство позволяет легко (фактически при помощи бинарного деления) найти все фрагменты кривой, "накрывающей" заданных AABB.

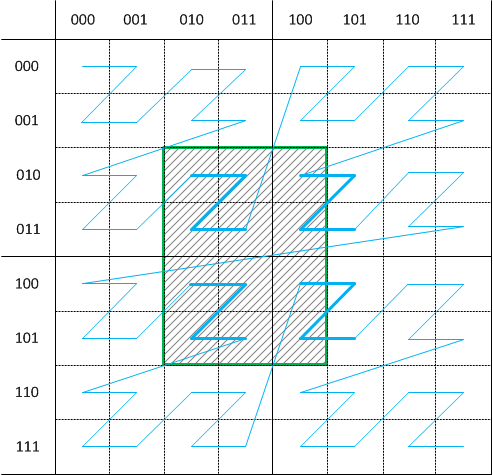
Рис 7. Поиск по кривой Мортона.

Собственно именно это и было первым применением кривых Мортона - организация хранения и поиска многомерных данных при помощи обычных СУБД (основанных обычно на упорядочивании элементов и использовании Б-дерева).

Для этого вводится достаточно большая сетка 2ⁿx2ⁿ(для двухмерных данных) и каждому объекту сопоставляется какой-либо узел решетки (например, содержащий центр его AABB). Тем самым каждому объекту можно сопоставить код Мортона, соответствующий данному узлу решетки. Далее именно этот код и используется для поиска элементов по базе данных.

Каждый запрос к базе (найти все объекты, попадающие в заданную область) сводится к определению соответствующий фрагментов кривой Мортона, т.е. нескольких отрезков содержащий интересующие коды Мортона. Сам поиск объектов по набору отрезков для кодов легко реализуется средствами баз данных (естественно, что найденные объекты потребуют более детальной проверки).

Еще одним примером применения кривой Мортона было параллельное построение иерархии ограничивающих объемов (BVH) для очень большого исходного набора объектов. Здесь также каждому объекту сопоставляется код Мортона, после чего список объектов параллельно сортируется по этому коду (например, при помощи параллельной поразрядной сортировки). Далее весь диапазон кодов разбивается на набор отрезков, каждому отрезку соответствует группа подряд идущих объектов в отсортированном списке. При удачно выборе точек разбиения (например, кратных заданной степени двойки) получающие группы объектов оказывается близко расположенными в пространстве и могут выступать основой для построения следующего уровня иерархии.

Кроме того, обход узлов решетки по кривой Мортона оказывается очень удачным с точки зрения кэширования - для GPU текстурный кэш двухмерен и обход по кривой Мортона очень выгоден. При работе с базами данных, отдельные участки (соответствующие блокам исходной решетки размером 2^kx2^k) могут размещаться в соседних блоках на диске, что опять делает обход по кривой очень выгодным.

Дополнительная информация:

Статья в Wiki по space-filling curves.

Статья в Wiki по кривой Мортона.

Статья в Wiki по кривой Мура.

Статья в Wiki по кривой Гильберта.

Статья в Wiki по кривой Серпинского