

|
Главная
 Статьи
Статьи
 Ссылки
Ссылки
 Скачать
Скачать
 Скриншоты
Скриншоты
 Юмор
Юмор
 Почитать
Почитать
 Tools
Tools
 Проекты
Проекты
 Обо мне
Обо мне
 Гостевая
Гостевая
 Форум
Форум


|
Распространение GPU, поддерживающих аппаратную тесселляцию, требует алгоритмов, позволяющих достаточно эффективно проводить тесселляцию набора треугольников. Обычно считается, что в каждой вершине такого треугольника задан единичный вектор нормали, который также используется при тесселляции.
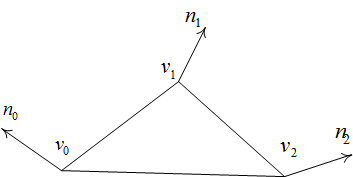
Рис 1. Исходный треугольник.
Далее мы рассмотрим два простых метода тесселляции и их реализацию при помощи тесселляционных шейдеров.
Данный алгоритм по вершинам и нормалям в них строит два треугольных патча Безье - кубический и квадратичный. Кубический патч используется для нахождения координат вершин, получающихся при тесселляции, а квадратичный - для нахождения нормалей в этих вершинах.
Пусть у нас есть треугольник с вершинами v0v1v2 и нормалями n0n1n2. Вся работа с треугольником будет проводиться в барицентрических координатах u, v и w (u+v+w=1, u,v,w >= 0).
Тогда кубическая патч Безье задается следующим уравнением.
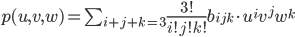
При этом все коэффициенты bijk разбиваются на три группы (см. рис. 2).
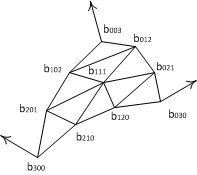
Рис 2. Коэффициенты кубического патча Безье.
В качестве значений коэффициентов в вершинах мы возьмем сами эти вершины:
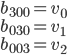
Для нахождения касательных коэффициентов bijk мы сперва найдем промежуточную точку (iv0+jv1+kv2)/3. Далее эта точка проектируется на плоскость, проходящую через ближайшую вершину. Такая плоскость задается уравнением (p-vi,ni)=0.
Тогда проекцию произвольной точки p на эту плоскость задается следующей формулой:
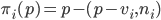
В результате мы получаем следующие уравнения для касательных коэффициентов:
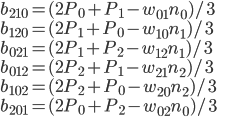
Коэффициенты wij определяются из следующего уравнения:
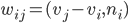
Коэффициент в центре b111 находится по следующей формуле:
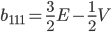
Здесь величины E и V задаются следующим образом:

Для нахождения нормали в точках разбиения используется квадратичный патч Безье (см. рис 3).
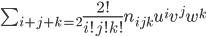
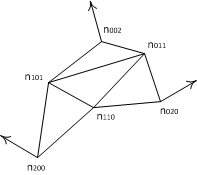
Рис 3. Коэффициенты квадратичного патча Безье.
Коэффициенты nijk соответствующие вершинам, берутся равными нормалям в вершинах.
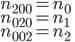
Остальные коэффициенты определяются следующим образом:
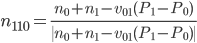
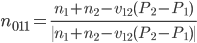
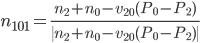
Коэффициенты vij задаются следующим уравнением:
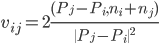
Для реализации данного способа тесселляции мы в tessellation control шейдере для каждого входного треугольника вычисляем все коэффициенты bijk и nijk и передаем в tessellation evaluation шейдер, который находит положения вершин и нормали в них используя найденные коэффициентов.
Соответствующие шейдеры приводятся ниже. Полный код ко всем примерам можно найти по ссылке в конце статьи.
-- vertex
#version 420 core
uniform mat4 mv;
uniform mat3 nm;
in vec3 position;
in vec3 normal;
out vec3 n;
void main(void)
{
gl_Position = mv * vec4 ( position, 1.0 );
n = normalize ( nm * normal );
}
-- tesscontrol
#version 420 core
uniform int inner;
uniform int outer;
in vec3 n [];
patch out vec3 b_300; // Bezier patch coefficients for vertices
patch out vec3 b_030;
patch out vec3 b_003;
patch out vec3 b_210;
patch out vec3 b_120;
patch out vec3 b_021;
patch out vec3 b_012;
patch out vec3 b_102;
patch out vec3 b_201;
patch out vec3 b_111;
patch out vec3 n_200; // Bezier coefficients for normals
patch out vec3 n_020;
patch out vec3 n_002;
patch out vec3 n_110;
patch out vec3 n_011;
patch out vec3 n_101;
layout(vertices = 3) out;
float w ( int i, int j )
{
return dot ( gl_in [j].gl_Position.xyz - gl_in [i].gl_Position.xyz, n [i] );
}
vec3 bb ( int i, int j )
{
return (2.0*gl_in [i].gl_Position.xyz + gl_in [j].gl_Position.xyz - w ( i, j ) * n [i]) / 3.0;
}
float lengthSq ( const vec3 v )
{
return dot ( v, v );
}
vec3 nn ( int i, int j )
{
vec3 dv = gl_in [j].gl_Position.xyz - gl_in [i].gl_Position.xyz;
vec3 vij = 2.0*( dv, n [i] + n [j] ) / lengthSq ( dv );
vec3 nij = n [i] + n [j] - vij * dv;
return normalize ( nij );
}
void main(void)
{
gl_TessLevelInner [0] = inner;
gl_TessLevelInner [1] = inner;
gl_TessLevelOuter [0] = outer;
gl_TessLevelOuter [1] = outer;
gl_TessLevelOuter [2] = outer;
gl_TessLevelOuter [3] = outer;
gl_out [gl_InvocationID].gl_Position = gl_in [gl_InvocationID].gl_Position;
b_300 = gl_in [0].gl_Position.xyz;
b_030 = gl_in [1].gl_Position.xyz;
b_003 = gl_in [2].gl_Position.xyz;
b_210 = bb ( 0, 1 );
b_120 = bb ( 1, 0 );
b_021 = bb ( 1, 2 );
b_012 = bb ( 2, 1 );
b_102 = bb ( 2, 0 );
b_201 = bb ( 0, 2 );
b_111 = 1.5*(b_210 + b_120 + b_021 + b_012 + b_102 + b_201) / 6.0 -
0.5*(gl_in [0].gl_Position.xyz + gl_in [1].gl_Position.xyz + gl_in [2].gl_Position.xyz) / 3.0;
n_200 = n [0];
n_020 = n [1];
n_002 = n [2];
n_110 = nn ( 0, 1 );
n_011 = nn ( 1, 2 );
n_101 = nn ( 2, 0 );
}
-- tesseval
#version 420 core
uniform mat4 proj;
in vec3 nn [];
out vec3 normal;
patch in vec3 b_300; // Bezier patch coefficients for vertices
patch in vec3 b_030;
patch in vec3 b_003;
patch in vec3 b_210;
patch in vec3 b_120;
patch in vec3 b_021;
patch in vec3 b_012;
patch in vec3 b_102;
patch in vec3 b_201;
patch in vec3 b_111;
patch in vec3 n_200; // Bezier coefficients for normals
patch in vec3 n_020;
patch in vec3 n_002;
patch in vec3 n_110;
patch in vec3 n_011;
patch in vec3 n_101;
layout(triangles, equal_spacing) in;
void main(void)
{
float u = gl_TessCoord.x;
float v = gl_TessCoord.y;
float w = gl_TessCoord.z;
vec3 p = (b_300*u + 3.0*b_210*v + 3.0*b_201*w)*u*u + (b_030*v + 3.0*b_120*u + 3.0*b_021*w)*v*v +
(b_003*w + 3.0*b_012*v + 3.0*b_102*u)*w*w + 6.0*b_111*u*v*w;
vec3 n = n_200*u*u + n_020*v*v + n_002*w*w + 2.0*n_110*u*v + 2.0*n_011*v*w + 2.0*n_101*u*w;
gl_Position = proj * vec4 ( p, 1.0 );
normal = normalize ( n );
}
-- fragment
#version 420 core
out vec4 color;
void main(void)
{
color = vec4(1.0);
}
Основная идея тесселляции Фонга довольно проста - по барицентрическим координатам u, v и w находится промежуточная точка P'.
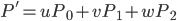
Далее через каждую вершину vi проводится касательная плоскость (используя вектор нормали в вершине как нормаль к плоскости) и точка P' проектируется на каждую из трех получившихся плоскостей (см. рис 4)).
После этого получившиеся точки умножаются на веса u, v, w и складываются давая искомое положение вершины, соответствующее данным барицентрическим координатам.
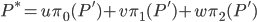
Нормаль в этой точке находится так же как и при закрашивании Фонга -
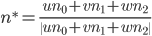
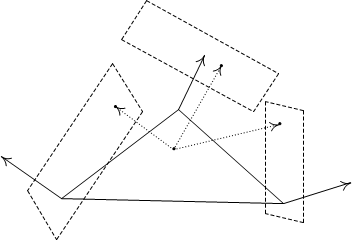
Рис 4. Проекции промежуточной точки P' на касательные плоскости в вершинах.
//
// Phong tessellation
//
-- vertex
#version 410 core
uniform mat4 mv;
uniform mat3 nm;
in vec3 position;
in vec3 normal;
out vec3 n;
void main(void)
{
gl_Position = mv * vec4 ( position, 1.0 );
n = normalize ( nm * normal );
}
-- tesscontrol
#version 410 core
uniform int inner;
uniform int outer;
in vec3 n [];
out vec3 nn [];
layout(vertices = 3) out;
void main(void)
{
gl_TessLevelInner [0] = inner;
gl_TessLevelInner [1] = inner;
gl_TessLevelOuter [0] = outer;
gl_TessLevelOuter [1] = outer;
gl_TessLevelOuter [2] = outer;
gl_TessLevelOuter [3] = outer;
gl_out [gl_InvocationID].gl_Position = gl_in [gl_InvocationID].gl_Position;
nn [gl_InvocationID] = n [gl_InvocationID];
}
-- tesseval
#version 410 core
uniform mat4 proj;
in vec3 nn [];
layout(triangles, equal_spacing) in;
void main(void)
{
float u = gl_TessCoord.x;
float v = gl_TessCoord.y;
float w = gl_TessCoord.z;
vec4 p = u * gl_in [0].gl_Position + v * gl_in [1].gl_Position + w * gl_in [2].gl_Position;
vec3 n = normalize ( u * nn [0] + v * nn [1] + w * nn [2] );
vec4 p0 = p - dot ( p.xyz - gl_in [0].gl_Position.xyz, nn [0] ) * vec4 ( nn [0], 0.0 );
vec4 p1 = p - dot ( p.xyz - gl_in [1].gl_Position.xyz, nn [1] ) * vec4 ( nn [1], 0.0 );
vec4 p2 = p - dot ( p.xyz - gl_in [2].gl_Position.xyz, nn [2] ) * vec4 ( nn [2], 0.0 );
gl_Position = proj * ( u * p0 + v * p1 + w * p2 );
}
-- fragment
#version 410 core
out vec4 color;
void main(void)
{
color = vec4(1.0);
}
По этой ссылке можно скачать весь исходный код к этой статье. Также доступны для скачивания откомпилированные версии для M$ Windows и Linux.