

|
Главная
 Статьи
Статьи
 Ссылки
Ссылки
 Скачать
Скачать
 Скриншоты
Скриншоты
 Юмор
Юмор
 Почитать
Почитать
 Tools
Tools
 Проекты
Проекты
 Обо мне
Обо мне
 Гостевая
Гостевая
 Форум
Форум


|
Это первая статья, посвященная рендерингу облаков на основе объемного (volumetric, voxel) представления. В ней будет рассматриваться сам процесс задания и рендеринга для сильно упрощенной модели. Далее я планирую сделать продолжение и рассказать о рендеринге облаков на основе того, как это было сделано в игре Horizon: Zero Dawn.
Принципиальным отличием облаков (а также тумана, дыма и т.п.) является то, что это объемный феномен, т.е. он определяется не границей, определяющий некоторый объем (когда важна именно граница), а содержимым этого объема. При этом зачастую точно провести эту границу просто невозможно.
Фактически облако представляет собой скопление маленьких капелек воды в воздухе. При прохождении через него лучи света, попадая в эти капельки, могут рассеиваться, давая в результате то, что мы обычно видим. Важно то, что размер этих капелек заметно больше длины волны \( \lambda \). При столкновении луча света с частицей может произойти поглощение (absorption) и рассеивание (scattering) света.
Фактически облако задается функцией распределения плотности (density) в пространстве. Ненулевая плотность соответствует облаку, нулевая - пустому пространству. При этом не очевидно как именно рассчитывать освещение - нет ни явной поверхности (на которой традиционно считается освещенность), ни нормали к ней - есть только плотность, которую мы будем обозначать \( \sigma \).
Под плотностью \( \sigma \) фактически понимается вероятность того, что луч света, пройдя единичное расстояние, будет поглощен ( \( \sigma_a \) ) или рассеян ( \( \sigma_s \) ). Через \( \sigma_t = \sigma_a + \sigma_s \) обозначается общая вероятность того, что луч света будет отклонен в сторону или поглощен.
Для учета света, идущего в заданном направлении мы должны учитывать не только поглощение света, но и in- и out-scattering, когда свет, идущий из другого направления в результате рассеивания уходит в интересующем нас направлении (рис 1).
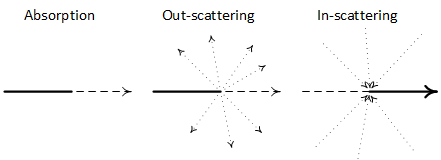
Рис 1. Рассеивание и его виды
Для того, чтобы понять как именно выполнять рендеринг облаков и рассчитывать освещение нам понадобятся два понятия из физики - закон Бира-Ламберта и фазовая функция (phase function).
Обратите внимание, что рассматриваемый ниже подход можно применить также и для расчета цвета неба, только в этом случае нужно рассматривать два вида рассеивания - Рэлея (от молекул воздуха с размером меньше длины волны) и Ми (от мелких частиц, заметно больших длины волны). Но формулы для рассеивания те же самые.
Закон Бира-Ламберта (Beer-Lambert) отвечает за поглощение света при прохождении через среду с ненулевой плотностью. Когда луч света проходит через среду с ненулевой оптической плотностью, то происходит поглощение света по экспоненциальному закону, именно этот закон и называется законом Бира-Ламберта. Проще всего этот закон выглядит в случае постоянной плотности \( \sigma \):
\[T=e^{-\sigma \cdot t}\]
Здесь через t обозначено пройденное в среде расстояние, а через \( \sigma \)- оптическая плотность среды ( \( \sigma_t \)). В общем случае (когда оптическая плотность является некоторой функцией), ослабление света задается следующей формулой:
\[ T = e ^ {- \int \sigma dt} \]
На рис. 2 приведен график получаемой функции.
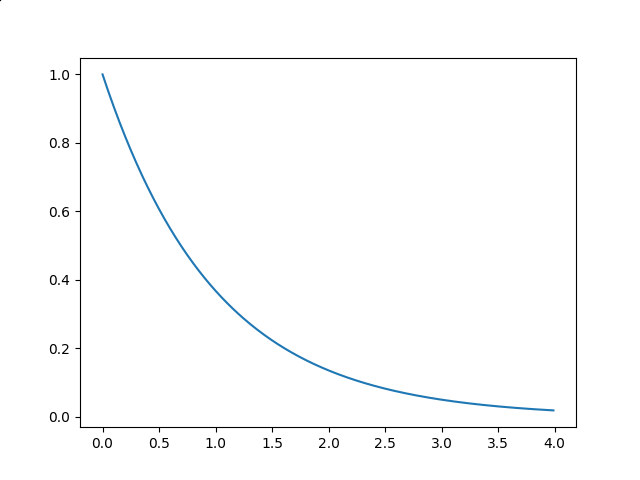
Рис 2. Поглощение света в зависимости от пройденного расстояния согласно закону Бира-Ламберта
Кроме поглощения света имеет место рассеивание света - когда луч сталкивается с микрочастицей (капелькой воды в случае облака), то происходит рассевание света - свет рассеивается по разным направлениям (рис 3). При этом обычно имеет место анизотропное рассеивание, т.е. световая энергия рассеивается не равномерно во все стороны. Тогда рассеивание световой энергии описывается так называемой фазовой функцией \( p \). Фактически фазовая функция \( p(\omega, \omega') \) задает угловое распределение рассеянного света. Поэтому справедливо условие нормировки:
\[ \int p(\omega, \omega' ) d\omega' = 1 \]
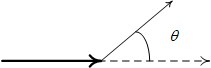
Рис 3. Рассеивание света
В большинстве поглощающих или рассеивающих сред фазовая функция зависит только от угла рассеивания \( \theta \). Одной из наиболее распространенных фазовых функций является функция Хеньи-Гринштейна (Henyey-Greenstein), задаваемая следующей формулой:
\[ p(\theta) = \frac{1}{4 \pi} \frac{1 - g^2}{(1 + g^2 + 2g \cos \theta) ^ {3/2}} \]
Здесь через g обозначен параметр анизотропии (или параметр асcиметрии), определяющий рассеивание. Он принимает значения из интервала \( (-1,1) \). Мы будем далее использовать именно эту функцию с параметром анизотропии равным 0.3. Иногда в качестве фазовой функции для облака используется сумма нескольких функций Хеньи-Гринштейна с разными значениями параметра g.

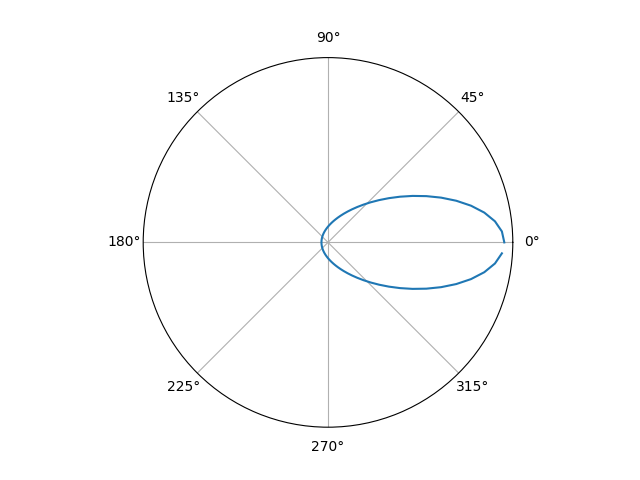
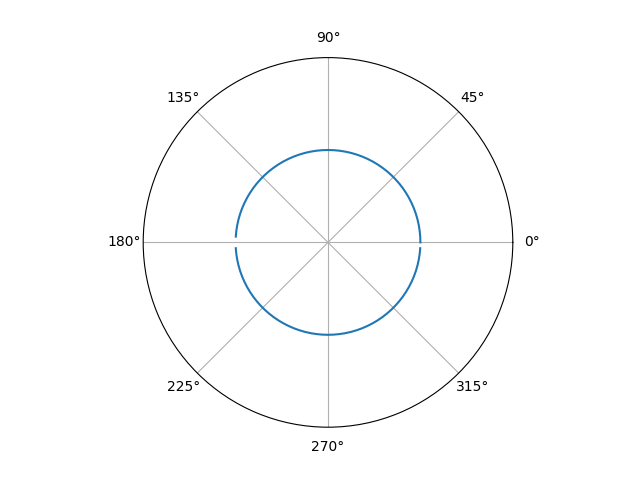
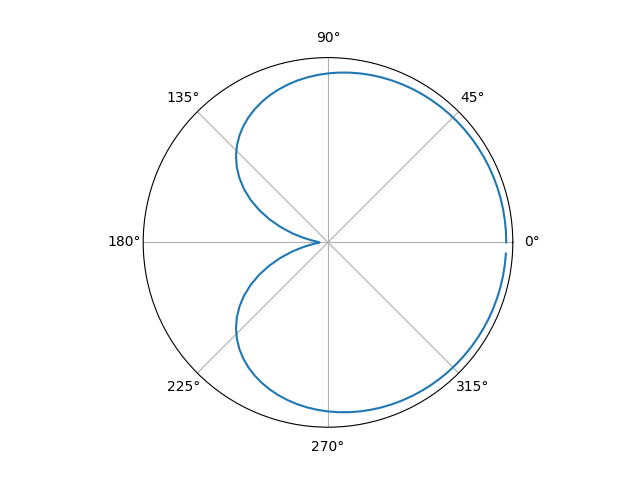
Рис 4. График фазовой функции Хеньи-Гринштейна для различных значений параметра g (0.3, 0.5, 1.0, 2.0).
Таки образом если в некоторой точке P мы хотим определить освещение, то мы из этой точки выпускаем луч к источнику света (Солнцу). Угол \( \theta \) между этим лучом и исходным лучом от камеры это тот самый угол из фазовой функции, которая определяет какая часть световой энергии, дошедшей до этой точки от Солнца, рассеется в направлении камеры. Также нужно учесть, что не вся световая энергия дойдет до точки P - часть ее будет поглощена в соответствие с законом Бира-Ламберта. Поэтому чтобы определить какая часть световой энергии дойдет до точки P мы идем вдоль луча к Солнцу с некоторым шагом и считаем поглощение (рис 5).
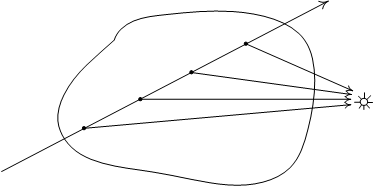
Рис 5. Расчет освещения вдоль луча
При этом, поскольку само облако является полупрозрачным, то мы будем идти вдоль луча с некоторым шагом, проверяя плотность. Если в точке Pi она равна нулю, то это значит, что здесь рассеивания света не происходит, и мы переходим к следующей точке Pi+1. Если плотность больше нуля, то мы находимся внутри облака и в этой точке происходит рассеивание света, часть которого уходит в интересующем нас направлении. Сколько из этого рассеянного света в точке Pi дойдет до нас определяется итоговой плотностью вдоль луча до этой точки. Перебирая таким образом точки вдоль луча с некоторым шагом, мы получим итоговую освещенность (рис 5).
Прежде чем писать полноценный рендеринг облаков с данной схемой расчета освещения, давайте сначала рассмотрим написание простейшего варианта, где освещение вообще не учитывается и мы рассматриваем только полупрозрачность.
Для начала нам нужно определить как именно мы будем задавать само облако, а точнее плотность внутри него. На самом деле облака удобно задавать при помощи SDF. Пусть в начале у нас есть SDF для сферы. Мы можем считать, что облако - это часть пространства, где значение функции меньше нуля. Тогда SDF, взятую с обратным знаком, можно рассматривать как плотность. То, что мы получаем при этом, вполне соответствует ожиданиям - у самой границы сферы плотность минимальна, по мере приближения к центру сферы плотность будет возрастать.
Но если мы берем только SDF от сферы (или нескольких сфер), то у нас получается слишком "правильное" облако - в жизни таких правильных облаков просто не бывает. Поэтому давайте добавим в SDF несколько октав шумовой функции, т.е. фактически добавим функцию fBm (fractal Brownian motion). Хотя строго говоря итоговая функция не является SDF (т.е. она не задает точно расстояние до поверхности уровня), но она дает подходящее распределение плотности и вполне качественное облако.
const float noiseSpaceScale = 0.5;
const float fbmScale = 1.3;
const vec3 timeScale = 0.03 * vec3 ( 1.0, -0.2, -1.0 );
const float texSize = 32.0;
const float PI = 3.1415926;
float BeersLaw ( float dist, float absorption )
{
return exp ( -dist * absorption );
}
float pow15 ( float x )
{
return x * sqrt ( x );
}
float HenyeyGreenstein ( float g, float mu )
{
float g2 = g * g;
return (1.0 / (4.0 * PI)) * ( (1.0 - g2) / pow15 ( 1.0 + g2 - 2.0 * g * mu ) );
}
float sdSphere ( vec3 p, vec3 center, float radius )
{
return length ( p - center ) - radius;
}
float noise3D ( vec3 p )
{
return textureLod ( noiseMap, p, 0 ).r * 2.0 - 1.0;
}
float fBm ( vec3 p )
{
vec3 q = p + time * timeScale;
float f = 0.0;
float scale = 0.51;
float factor = 2.02;
for ( int i = 0; i < 4; i++ )
{
f += scale * noise3D ( q );
q *= factor;
factor += 0.21;
scale *= 0.5;
}
return f;
}
float fBm ( vec3 p, bool lowRes )
{
vec3 q = p + time * 0.03 * vec3 ( 1.0, -0.2, -1.0 );
float f = 0.0;
float scale = 0.51;
float factor = 2.02;
int numOctaves = lowRes ? 4 : 3;
for ( int i = 0; i < numOctaves; i++ )
{
f += scale * noise3D ( q );
q *= factor;
factor += 0.21;
scale *= 0.5;
}
return f;
}
float scene ( vec3 p, bool lowRes )
{
p *= mv;
float d1 = sdSphere ( p, vec3 ( 0, -1, 0.3 ), 1.3 );
float d2 = sdSphere ( p, vec3 ( 0, 1.2, 0 ), 1.5 );
float distance = min ( d1, d2 );
float f = fBm ( noiseSpaceScale * p, lowRes );
return -distance + fbmScale * f;
}
Далее мы для каждого фрагмента выпускаем луч в сцену как и при рендеринге SDF и трассируем его (вот здесь уже будут отличия от рендеринга SDF). Проще всего с самого начала идти вдоль луча с постоянным шагом. Проблема только в том, что при таком подходе у нас в начале будет очень много пустых точек, в каждой из которых мы должны вычислить нашу функцию сцены. А это не самый лучший вариант с точки зрения быстродействия. Лучше вспомнить у функция сцены это "как-бы" SDF и выполнить вначале несколько шагов аналогично рендерингу SDF. И только когда мы уже близко подойдем к нашему облаку можно начинать идти вдоль луча с постоянным шагом.
#define MAX_STEPS 100
#define MARCH_SIZE 0.16
#include "clouds-inc.glsl"
vec4 raymarch ( vec3 rayOrigin, vec3 rayDirection, float offset )
{
float depth = offset * MARCH_SIZE;
vec4 res = vec4 ( 0.0 );
float maxDepth = MAX_STEPS * MARCH_SIZE;
while ( depth < maxDepth )
{
vec3 p = rayOrigin + depth * rayDirection;
float density = scene ( p, false );
if ( density < -MARCH_SIZE )
{
depth += -density*0.5;
continue;
}
// We only draw the density if it's greater than 0
if ( density > 0.0 )
{
vec4 color = vec4 ( mix ( vec3(1.0), vec3(0.0), density ), density );
color.rgb *= color.a;
res += color * (1.0 - res.a);
}
depth += MARCH_SIZE;
}
return res;
}
void main()
{
float blueNoise = texture ( blueNoiseMap, uv ).r;
vec3 org = vec3 ( 0.0, 0.0, 5.0 ); // Ray Origin - camera
vec3 dir = normalize ( vec3 ( p.xy, -1.0 ) ); // Ray Direction
vec4 res = raymarch ( org, dir, fract ( blueNoise + time ) * 0.5 );
color = vec4 ( res.rgb, 1 );
}
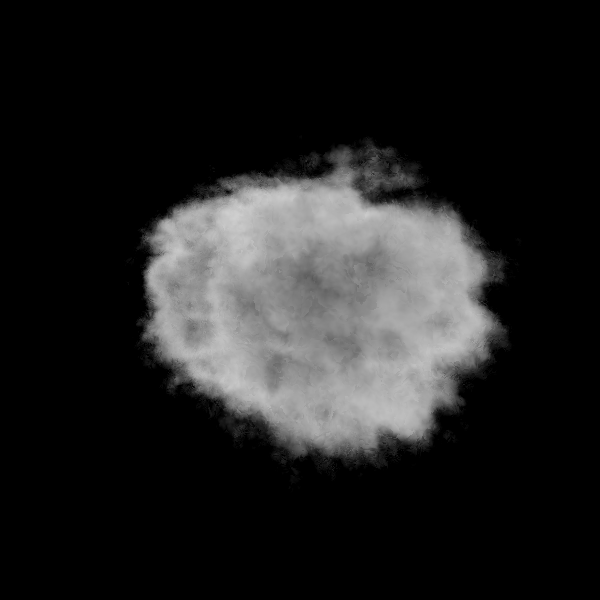
Рис 6. Облако без освещения
Теперь, имея базовый работающий код для рендеринга облака, мы можем подключить использование освещения, по рассмотренной ранее схеме. Проще вынести расчет освещения в точке в отдельную функцию, в результате мы приходим к следующему коду
#version 330 core
uniform vec3 eye;
uniform mat3 mv;
uniform float time;
uniform sampler3D noiseMap;
uniform sampler2D blueNoiseMap;
in vec2 uv;
in vec3 p;
out vec4 color;
#define MAX_STEPS 50
#define MAX_SUN_STEPS 6
#define MARCH_SIZE 0.16
#define ABSORPTION_COEFFICIENT 0.9
#define SCATTERING_ANISO 0.3
const vec3 sunDirection = normalize ( vec3 ( 1.0, 0.0, 0.0 ) );
const vec3 sunColor = vec3 ( 1.0,0.5,0.3 );
const float lighScale = 2;
#include "clouds-inc.glsl"
float lightmarch ( vec3 pos, vec3 lightDir )
{
float totalDensity = 0.0;
float marchSize = 0.03;
for ( int step = 0; step < MAX_SUN_STEPS; step++ )
{
pos += lightDir * marchSize * float ( step );
totalDensity += scene ( pos, true );
}
float transmittance = BeersLaw ( totalDensity, ABSORPTION_COEFFICIENT );
return transmittance;
}
float raymarch ( vec3 rayOrigin, vec3 rayDirection, float offset )
{
float depth = offset * MARCH_SIZE;
float maxDepth = MAX_STEPS * MARCH_SIZE;
float totalTransmittance = 1.0;
float lightEnergy = 0.0;
float phase = HenyeyGreenstein ( SCATTERING_ANISO, dot ( rayDirection, sunDirection ) );
while ( depth < maxDepth )
{
vec3 p = rayOrigin + depth * rayDirection;
float density = scene ( p, false );
if ( density < -MARCH_SIZE )
{
depth += -density*0.5;
continue;
}
// We only draw the density if it's greater than 0
if ( density > 0.0 )
{
float lightTransmittance = lightmarch ( p, sunDirection ); //????
float luminance = 3*0.05 + density * phase * lighScale;
totalTransmittance *= lightTransmittance;
lightEnergy += totalTransmittance * luminance;
}
depth += MARCH_SIZE;
}
return 14*0.05 * lightEnergy;
}
void main()
{
float blueNoise = texture ( blueNoiseMap, uv ).r;
vec3 org = vec3 ( 0.0, 0.0, 5.0 ); // Ray Origin - camera
vec3 dir = normalize ( vec3 ( p.xy, -1.0 ) ); // Ray Direction
float res = raymarch ( org, dir, fract ( blueNoise + time ) * 0.5 );
color = vec4 ( res * sunColor, 1 );
}
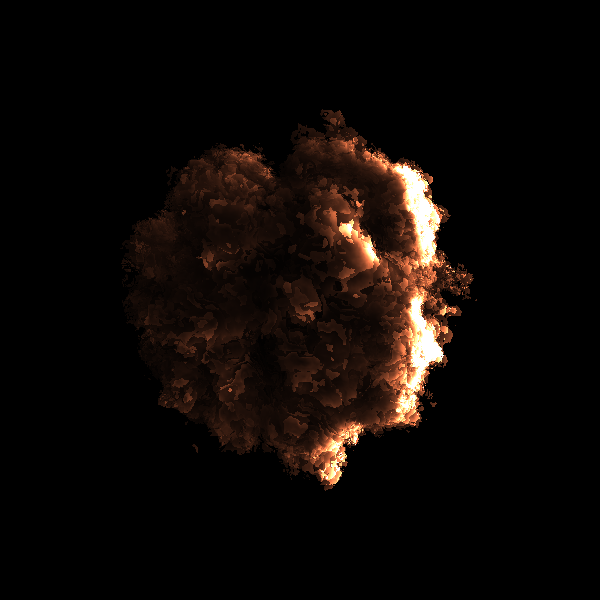
Рис 7. Облако с освещением
Как несложно убедиться расчет облака с освещением является довольно ресурсоемким делом. Можно повысить быстродействие, если увеличить шаг, с которым мы идем вдоль луча. Однако если мы просто заметно увеличим этот шаг, это может привести к заметным визуальным артефактам.
Стандартным приемом в компьютерной графике для снижения заметности подобных артефактов является добавление небольшого шума (jitter). Проще всего реализовать это следующим образом - мы для каждого трассируемого луча будем смещать стартовую точку вдоль луча на небольшое случайное значение.
Поскольку честных случайных чисел (или даже готового генератора псевдослучайных чисел) на GPU нет, то мы будем использовать для этого заранее подготовленную текстуру с шумом, довольно хорошие результаты дает использование так называемого синего шума (blue noise).

Рис 8. Синий шум
В зависимости от текущего фрагмента мы будем извлекать из этой текстуры значение шума. Также имеет смысл добавить зависимость от времени - для этого мы можем просто использовать дробную часть текущего времени. Сложив эти два значения и умножив их на шаг вдоль луча мы и получим случайное смещение стартовой точки.
#version 330 core
uniform vec3 eye;
uniform mat3 mv;
uniform float time;
uniform sampler3D noiseMap;
uniform sampler2D blueNoiseMap;
in vec2 uv;
in vec3 p;
out vec4 color;
#define MAX_STEPS 50
#define MAX_SUN_STEPS 6
#define MARCH_SIZE 0.16
#define ABSORPTION_COEFFICIENT 0.9
#define SCATTERING_ANISO 0.3
#define PI 3.1415926
const vec3 SUN_POSITION = normalize ( vec3 ( 1.0, 0.0, 0.0 ) );
const vec3 sunColor = vec3 ( 1.0,0.5,0.3 );
float sdSphere ( vec3 p, float radius )
{
return length ( p ) - radius;
}
float noise3D ( vec3 p )
{
return textureLod ( noiseMap, p, 0.0 ).r * 2.0 - 1.0;
}
float fBm ( vec3 p, bool lowRes )
{
vec3 q = p + time * 0.1 * vec3 ( 1.0, -0.2, -1.0 );
float f = 0.0;
float scale = 0.5;
float factor = 2.02;
int numOctaves = lowRes ? 4 : 3;
for ( int i = 0; i < numOctaves; i++ )
{
f += scale * noise3D ( q );
q *= factor;
factor += 0.21;
scale *= 0.5;
}
return f;
}
float scene ( vec3 p, bool lowRes )
{
p *= mv;
float distance = sdSphere ( p, 1.0 );
float f = fBm ( p, lowRes );
return -distance + f;
}
float BeersLaw ( float dist, float absorption )
{
return exp ( -dist * absorption );
}
float pow15 ( float x )
{
return x * sqrt ( x );
}
float HenyeyGreenstein ( float g, float mu )
{
float g2 = g * g;
return (1.0 / (4.0 * PI)) * ( (1.0 - g2) / pow15 ( 1.0 + g2 - 2.0 * g * mu ) );
}
float lightmarch ( vec3 pos, vec3 dir )
{
vec3 lightDir = SUN_POSITION;
float totalDensity = 0.0;
float marchSize = 0.03;
for ( int step = 0; step < MAX_SUN_STEPS; step++ )
{
pos += lightDir * marchSize * float ( step );
float lightSample = scene ( pos, true );
totalDensity += lightSample;
}
float transmittance = BeersLaw ( totalDensity, ABSORPTION_COEFFICIENT );
return transmittance;
}
float raymarch ( vec3 rayOrigin, vec3 rayDirection, float offset )
{
float depth = offset * MARCH_SIZE;
float maxDepth = MAX_STEPS * MARCH_SIZE;
vec3 sunDirection = normalize ( SUN_POSITION );
float totalTransmittance = 1.0;
float lightEnergy = 0.0;
float phase = HenyeyGreenstein ( SCATTERING_ANISO, dot ( rayDirection, sunDirection ) );
while ( depth < maxDepth )
{
vec3 p = rayOrigin + depth * rayDirection;
float density = scene ( p, false );
if ( density < -MARCH_SIZE )
{
depth += -density*0.5;
continue;
}
// We only draw the density if it's greater than 0
if ( density > 0.0 )
{
float lightTransmittance = lightmarch ( p, sunDirection );
float luminance = 0.025 + density * phase;
totalTransmittance *= lightTransmittance;
lightEnergy += totalTransmittance * luminance;
}
depth += MARCH_SIZE;
}
return lightEnergy;
}
void main()
{
float blueNoise = texture ( blueNoiseMap, uv ).r;
vec3 org = vec3 ( 0.0, 0.0, 5.0 ); // Ray Origin - camera
vec3 dir = normalize ( vec3 ( p.xy, -1.0 ) ); // Ray Direction
float res = raymarch ( org, dir, fract ( blueNoise + time ) * 0.5 );
// Sun and Sky
vec3 sunColor = vec3 ( 1.0,0.5,0.3 );
vec3 sunDirection = normalize ( SUN_POSITION );
float sun = clamp ( dot ( sunDirection, dir), 0.0, 1.0 );
// Base sky color
color.rgb = vec3 ( 0.7, 0.7, 0.90 );
// Add vertical gradient
color.rgb -= 0.8 * vec3 ( 0.90, 0.75, 0.90 ) * dir.y;
// Add sun color to sky
color.rgb += 0.5 * sunColor * pow ( sun, 10.0 );
// Add cloud color
color = vec4 ( color.rgb + res * sunColor, 1 );
}

Рис 9. Облако с освещением и смещением стартовой точки вдоль луча.
В игре Horizon: Dawn при рендеринге облаков был использован еще один член при расчете освещения, получивший название powder term. Он отвечает за тот эффект, когда облако возле границы выглядит темнее. Физически этот эффект можно объяснить тем, что у точек, находящихся около границы, заметно меньше вклад рассеянного освещение по сравнению с точками, находящимися в глубине. Для описания этого эффекта была преложена следующая формула \[ E = e^{-d} (1 - e^{-2 d}) \]

Исходный код для этой статьи можно скачать https://github.com/steps3d/graphics-book/tree/master/Code/python-code.
Полезные ссылки:
Real-time Dreamy Cloudscapes with Volumetric Raymarching