Главная

Статьи

Ссылки

Скачать

Скриншоты

Юмор

Почитать

Tools

Проекты

Обо мне

Гостевая

Форум

Модели освещения

Основные обозначения

$n$ - единичный вектор нормали в точке.

$l$ - единичный вектор направления на источник света.

$v$ - единичный вектор направления на камеру (наблюдателя).

$h = \frac{l + v}{|l + v|}$ - биссектор векторов на источник света и камеру.

$\cos\theta_l=(n,l)$ - косинус угла между нормалью к поверхности в точке и направлением на источник света.

$\cos\theta_v=(n,v)$ - косинус угла между нормалью к поверхности в точке и направлением на камеру.

Ламберт

Простейшая модель освещения - чисто диффузное освещение. Считается, что свет падающий в точку, одинакового рассеивается по всем направлением полупространства. Таким образом, освещенность в точке определяется только плотностью света в точке поверхности, а она линейно зависит от косинуса угла падения.

$I=\max(0,(n,l))$

Для отсечения случая, когда косинус угла отрицателен, в уравнение включено отсечение значений косинуса, меньших нуля.

На скриншоте приведено изображение, получаемое при помощи этой модели. Ниже приводятся вершинный и фрагментный шейдеры на GLSL, реализующие данную модель освещения.

//
// Lambert vertex shader
//

varying vec3 l;
varying vec3 n;

uniform vec4 lightPos;
uniform vec4 eyePos;

void main(void)
{
    vec3 p = vec3 ( gl_ModelViewMatrix * gl_Vertex );           // transformed point to world space

    l = normalize ( vec3 ( lightPos ) - p );                    // vector to light source
    n = normalize ( gl_NormalMatrix * gl_Normal );              // transformed n

    gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}

//
// Lambert fragment shader
//

varying vec3 l;
varying vec3 n;

void main (void)
{
    const vec4 diffColor = vec4 ( 0.5, 0.0, 0.0, 1.0 );

    vec3 n2   = normalize ( n );
    vec3 l2   = normalize ( l );
    vec4 diff = diffColor * max ( dot ( n2, l2 ), 0.0 );

    gl_FragColor = diff;
}

Wrap-around

Также встречается небольшая модификация модели Ламберта, увеличивающая освещаемую область, за счет смещения f.

$I=\frac{\max(0,(n,l) + f)}{1+f}$

Чайник, освещенный при помощи модели освещения wrap-around.

Ниже приводится фрагментный шейдер, соответствующий данной модели освещения. Вершинный шейдер совпадает с вершинным шейдером для модели Ламберта.

//
// Wrap-around lighting fragment shader
//

varying vec3 l;
varying vec3 n;

void main (void)
{
    const vec4  diffColor = vec4 ( 0.5, 0.0, 0.0, 1.0 );
    const float factor    = 0.5;

    vec3 n2   = normalize ( n );
    vec3 l2   = normalize ( l );
    vec4 diff = diffColor * max ( dot ( n2, l2 ) + factor, 0.0 ) / ( 1.0 + factor );

    gl_FragColor = diff;
}

Фонг

Одной из самых распространенных моделей освещения, поддерживающих блики (specular hilights) является модель Фонга.

$I=\max(0,(l,r))^p$

Через r в этой модели обозначен вектор, получающийся при отражении вектора наблюдателя относительно нормали. Если все вектора единичные, то справедлива формула:

$r=2n(n,v)-v$

Ниже приводятся соответствующие вершинный и фрагментный шейдеры.

//
// Phong vertex shader
//

varying	vec3 l;
varying	vec3 v;
varying	vec3 n;

uniform	vec4	lightPos;
uniform	vec4	eyePos;

void main(void)
{
    vec3 p = vec3      ( gl_ModelViewMatrix * gl_Vertex );      // transformed point to world space

    l = normalize ( vec3 ( lightPos ) - p );                    // vector to light source
    v = normalize ( vec3 ( eyePos )   - p );                    // vector to the eye
    n = normalize ( gl_NormalMatrix * gl_Normal );              // transformed n

    gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}

//
// Phong fragment shader
//

varying vec3 l;
varying vec3 v;
varying vec3 n;

void main (void)
{
    const vec4  diffColor = vec4 ( 0.5, 0.0, 0.0, 1.0 );
    const vec4  specColor = vec4 ( 0.7, 0.7, 0.0, 1.0 );
    const float specPower = 30.0;

    vec3 n2   = normalize ( n );
    vec3 l2   = normalize ( l );
    vec3 v2   = normalize ( v );
    vec3 r    = reflect ( -v2, n2 );
    vec4 diff = diffColor * max ( dot ( n2, l2 ), 0.0 );
    vec4 spec = specColor * pow ( max ( dot ( l2, r ), 0.0 ), specPower );

    gl_FragColor = diff + spec;
}

Блинн

Еще одной достаточно распространенной моделью, дающей бликовое освещение, является модель Блинна.

$I=\max(0,(n,h))^p$

$h=\frac{l + v}{|l + v|}$

//
// Blinn fragment shader
//

varying	vec3 l;
varying	vec3 h;
varying vec3 v;
varying vec3 n;

void main (void)
{
    const vec4  diffColor = vec4 ( 0.5, 0.0, 0.0, 1.0 );
    const vec4  specColor = vec4 ( 0.7, 0.7, 0.0, 1.0 );
    const float specPower = 30.0;

    vec3 n2   = normalize ( n );
    vec3 l2   = normalize ( l );
    vec3 h2   = normalize ( h );
    vec4 diff = diffColor * max ( dot ( n2, l2 ), 0.0 );
    vec4 spec = specColor * pow ( max ( dot ( n2, h2 ), 0.0 ), specPower );

    gl_FragColor = diff + spec;
}

Изотропная модель Ward

Еще одной достаточно простой моделью, поддерживающей блики, является изотропная модель Варда. Бликовое освещение определяется по следующей формуле:

$I=\exp^{-k \frac{1-(h,n)^2}{(h,n)^2}}$

В этой формуле параметр k отвечает за неровность поверхности. Ниже приводится изображение чайника, освещенное при помощи э той модели.

//
// Isotropic Ward fragment shader
//

varying	vec3 l;
varying	vec3 h;
varying vec3 v;
varying vec3 n;

void main (void)
{
    const vec4  diffColor = vec4 ( 0.5, 0.0, 0.0, 1.0 );
    const vec4  specColor = vec4 ( 0.7, 0.7, 0.0, 1.0 );
    const float k         = 10.0;

    vec3  n2   = normalize ( n );
    vec3  l2   = normalize ( l );
    vec3  h2   = normalize ( h );
    float hn   = dot       ( h, n );
    float hn2  = hn * hn;

    vec4  diff = diffColor * max ( dot ( n2, l2 ), 0.0 );
    vec4  spec = specColor * exp ( - k * (1.0 - hn2) / hn2 );

    gl_FragColor = diff + spec;
}

Орен-Наяр

Модель освещения Ламберта хорошо работает только для сравнительно гладких поверхностей. В отличии от нее модель Орен-Найара основана на предположении, что поверхность состоит из множества микрограней, освещение каждой из которых описывается моделью Ламберта. Модель учитывает взаимное закрывание и затенение микрограней и также учитывает взаимное отражение света между микрогранями.

По этой модели, освещение задается следующей формулой:

$I=\cos(\theta_L)(A+B\max(0,\cos(\phi_V-\phi_L))\sin(\alpha)\tan(\beta))$

Параметры модели определяются по следующим формулам:

$A=1-0.5\frac{\sigma^2}{\sigma^2+0.33}$

$B=0.45\frac{\sigma^2}{\sigma^2+0.09}$

$\alpha=\min(\theta_L,\theta_V)$

$\beta=\max(\theta_L,\theta_V)$

Параметр $\sigma$ отвечает за неровность поверхности, чем он больше, тем более неровной является поверхность.

Ниже приводится изображение чайника, освещенное при помощи модели Орен-Найара.

На следующем листинге приведен фрагментный шейдер для модели освещения Орен-Найара.

//
// Oren-Nayar fragment shader
//

varying	vec3 l;
varying vec3 v;
varying vec3 n;

uniform	float a, b;

void main (void)
{
    const vec4 diffColor = vec4 ( 0.5, 0.0, 0.0, 1.0 );

    vec3  n2   = normalize ( n );
    vec3  l2   = normalize ( l );
    vec3  v2   = normalize ( v );

    float nl    = dot ( n2, l2 );
    float nv    = dot ( n2, v2 );
    vec3  lProj = normalize ( l2 - n2 * nl );
    vec3  vProj = normalize ( v2 - n2 * nv );
    float cx    = max ( dot ( lProj, vProj ), 0.0 );

    float cosAlpha = nl > nv ? nl : nv;
    float cosBeta  = nl > nv ? nv : nl;
    float dx       = sqrt ( ( 1.0 - cosAlpha * cosAlpha ) * ( 1.0 - cosBeta * cosBeta ) ) / cosBeta;

    gl_FragColor = max ( 0.0, nl ) * diffColor * (a + b * cx * dx);
}

Cook-Torrance

Одной из наиболее продвинутых и согласованных с физикой является модель освещение Кука-Торранса. Она также основана на модели поверхности состоящей из микрограней, каждая из которых является идеальным зеркалом. Модель учитывает коэффициент Френеля и взаимозатенение микрограней.

$I=\frac{FGD}{\pi(n,l)(n,v)}$

В данной модели (как и в модели Орен-Найара) считается что угол $\theta$ между нормалью к микрограни и нормалью ко всей поверхности является случайно величиной, подчиняющейся закону распределения Бэкмена:

$D_{Beckmen}=\frac{1}{m^2\cos^4\theta}\exp(-\frac{\tan^2\theta}{m^2})$

За затенение отдельных микрограней отвечает функция $G(n,l,v,h)$ :

$G=\min\left(1,\frac{2(n,h)(n,v)}{(v,h)},\frac{2(n,h)(n,l)}{(v,h)}\right)$

Ниже приводятся два изображения чайника, освещенные при помощи этой модели.

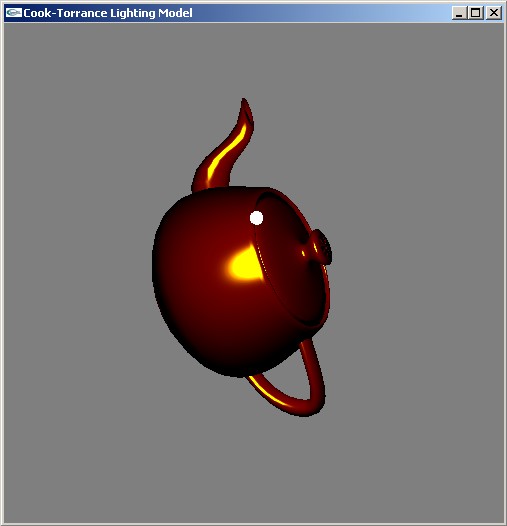
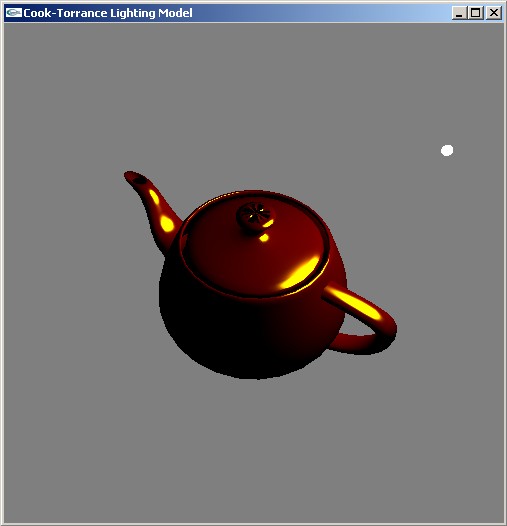
Ниже приводятся вершинный и фрагментный шейдеры для этой модели.

//
// Cook-Torrance vertex shader
//

varying	vec3 l;
varying	vec3 h;
varying	vec3 n;
varying vec3 v;

uniform	vec4	lightPos;
uniform	vec4	eyePos;

void main(void)
{
    vec3 p = vec3 ( gl_ModelViewMatrix * gl_Vertex );           // transformed point to world space

    l = normalize ( vec3 ( lightPos ) - p );                    // vector to light source
    v = normalize ( vec3 ( eyePos )   - p );                    // vector to the eye
    h = normalize ( l + v );
    n = normalize ( gl_NormalMatrix * gl_Normal );              // transformed n

    gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}

//
// Cook-Torrance fragment shader
//

varying	vec3 l;
varying	vec3 h;
varying vec3 v;
varying vec3 n;

uniform	float     r0;
uniform float     roughness;
uniform sampler2D lookupMap;

float fresnel ( float ca )
{
    return (r0 + (1.0 - r0)*pow ( 1.0 - ca, 5.0)) / ca;
}

void main (void)
{
    const vec4  diffColor = vec4 ( 0.5, 0.0, 0.0, 1.0 );
    const vec4  specColor = vec4 ( 0.7, 0.7, 0.0, 1.0 );
    const float e         = 2.7182818284;
    const float pi        = 3.1415926;

    vec3  n2   = normalize ( n );
    vec3  l2   = normalize ( l );
    vec3  v2   = normalize ( v );
    vec3  h2   = normalize ( h );
    float nh   = dot ( n2, h2 );
    float nv   = dot ( n2, v2 );
    float nl   = dot ( n2, l2 );
    float d    = texture2D ( lookupMap, vec2 ( roughness, nh ) ).x;
/*	
    float r2   = roughness * roughness;
    float nh2  = nh * nh;
    float ex   = - (1.0 - nh2)/(nh2 * r2);
    float d    = pow ( e, ex ) / (r2*nh2*nh2);
*/
    float f    = mix ( pow ( 1.0 - nv, 5.0 ), 1.0, r0 );		// Fresnel
    float x    = 2.0 * nh / dot ( v2, h2 );
    float g    = min ( 1.0, min ( x * nl, x * nv ) );			// Geometry attenuation
    float ct   = d*f*g / nv;

    vec4  diff = diffColor * max ( 0.0, nl );
    vec4  spec = specColor * max ( 0.0, ct );

    gl_FragColor = diff + spec;
}

Анизотропная модель

Все ранее рассмотренные модели являются изотропными, т.е. при повороте поверхности вокруг вектора нормали, освещение в точке не изменяется. Однако есть целый ряд материалов (например поверхность компакт-диска) для который это условие не выполняется.

Используемые для освещения подобных поверхностей модели называются анизотропными. При этом, для того чтобы можно было учитывать поворот грани вокруг вектора нормали, на поверхности нужно ввести поле касательных векторов, т.е. каждой точке поверхности сопоставляется касательный вектор, перпендикулярный нормали. По касательному вектору и нормали можно найти еще один вектор, перпендикулярный нормали, так называемую бинормаль.

Взятые вместе, нормаль, касательная и бинормаль образуют так называемый касательный базис.

Простейшая анизотропная модель освещения основана на довольно простой модели - вся поверхность считается состоящей из бесконечно тонких нитей. Тогда в качестве касательного вектора в точке выступает касательная к нити, проходящей через данную точку.

Модель освещения для отдельной нити основывается на модели Блинна или Фонга где в качестве нормали выступает вектор, перпендикулярный вектору нормали, и дающий наибольшее значение для диффузной и бликовой составляющих освещения.

$I_{diff}=\sqrt{1-(t,l)^2}$

$I_{spec}=(1-(t,l))^2)^{\frac{p}{2}}$

Ниже приводится изображение тора, освещенного при помощи этой модели.

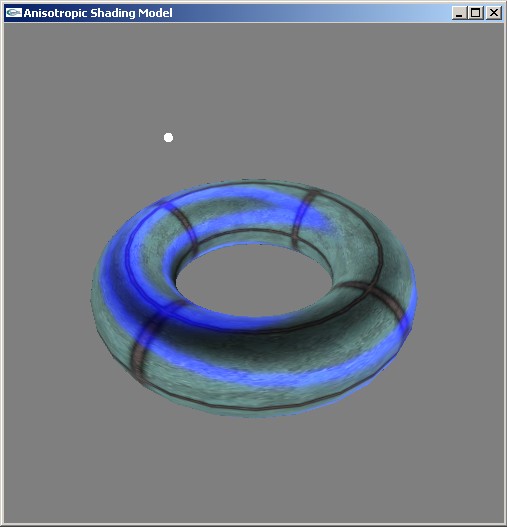
Ниже приводятся вершинный и фрагментный шейдеры, реализующие данную модель освещения.

//
// Simple anisotropic lighting vertex shader
//

varying	vec3 lt;
varying	vec3 ht;

uniform	vec4	lightPos;
uniform	vec4	eyePos;

void main(void)
{
    vec3 p = vec3      ( gl_ModelViewMatrix * gl_Vertex ); // transformed point to world space
    vec3 l = normalize ( vec3 ( lightPos ) - p );          // vector to light source
    vec3 v = normalize ( vec3 ( eyePos )   - p );          // vector to the eye
    vec3 h = normalize ( l + v );
    vec3 n = gl_NormalMatrix * gl_Normal;                  // transformed n
    vec3 t = gl_NormalMatrix * gl_MultiTexCoord1.xyz;      // transformed t
    vec3 b = gl_NormalMatrix * gl_MultiTexCoord2.xyz;      // transformed b

                                                           // now remap l, and h into tangent space
    lt = vec3 ( dot ( l, t ), dot ( l, b ), dot ( l, n ) );
    ht = vec3 ( dot ( h, t ), dot ( h, b ), dot ( h, n ) );

    gl_Position     = gl_ModelViewProjectionMatrix * gl_Vertex;
    gl_TexCoord [0] = gl_MultiTexCoord0;
}

//
// Simple anisotropic lighting fragment shader
//

varying	vec3 lt;
varying	vec3 ht;

uniform sampler2D tangentMap;
uniform sampler2D decalMap;
uniform sampler2D anisoTable;

void main (void)
{
    const vec4 specColor = vec4 ( 0, 0, 1, 0 );

    vec3  tang  = normalize ( 2.0 * texture2D ( tangentMap, gl_TexCoord [0].xy ).xyz - 1.0 );
    float dot1  = dot  ( normalize ( lt ), tang );
    float dot2  = dot  ( normalize ( ht ), tang );
    vec2  arg   = vec2 ( dot1, dot2 );
    vec2  ds    = texture2D ( anisoTable, arg*arg ).rg;
    vec4  color = texture2D ( decalMap, gl_TexCoord [0].xy );

	gl_FragColor   = color * ds.x + specColor * ds.y;
	gl_FragColor.a = 1.0;
}

Анизотропная модель Ward

Также существует анизотропный вариант модели освещения Варда, параметр k как и ранее отвечает за неровность поверхности.

$I=\exp^{-\left(k \frac{(h,t)}{(h,n)}\right)^2}$

Ниже приводится изображение тора, освещенного при помощи анизотропной модели Варда.

//
// Anisotropic Ward lighting fragment shader
//

varying vec3 vt;
varying	vec3 lt;
varying	vec3 ht;

uniform sampler2D tangentMap;
uniform sampler2D decalMap;

void main (void)
{
	const vec4	specColor = vec4 ( 0, 0, 1, 0 );
	const vec3	n         = vec3 ( 0, 0, 1 );
	const float	roughness = 5.0;

	vec4	color = texture2D ( decalMap, gl_TexCoord [0].xy );
	vec3	tang  = normalize ( 2.0 * texture2D ( tangentMap, gl_TexCoord [0].xy ).xyz - vec3 ( 1.0 ) );
	float	dot1  = dot  ( ht, tang ) * roughness;
	float	dot2  = dot  ( ht, n );
	float	p     = dot1 / dot2;

	gl_FragColor.rgb = color.rgb + specColor.rgb * exp ( -p*p );
	gl_FragColor.a   = 1.0;
}

Minnaert

Эта модель была предложена для моделирования освещения планет, также довольно хорошо она подходит для моделирования некоторых видов ткани, например вельвета.

$I=(n,l)^{1 + k}(1-(n,v))^{1-k}$

Ниже приводится изображение чайника, освещенного при помощи этой модели.

//
// Minnaert lighting model fragment shader
//
varying	vec3 l;
varying	vec3 h;
varying vec3 v;
varying vec3 n;

void main (void)
{
    const vec4  diffColor = vec4 ( 1.0, 1.0, 0.0, 1.0 );
    const float k         = 0.8;

    vec3  n2 = normalize ( n );
    vec3  l2 = normalize ( l );
    vec3  v2 = normalize ( v );
    float d1 = pow ( max ( dot ( n2, l2 ), 0.0 ), 1.0 + k );
    float d2 = pow ( 1.0 - dot ( n2, v2 ), 1.0 - k );

    gl_FragColor = diffColor * d1 * d2;
}

Ashikhmin-Shirley

Одной из наиболее сложных анизотропных моделей освещения является модель Ашихмина-Ширли. Ниже приводятся формулы для расчета диффузной и бликовой компонент.

$I_{diff}=\frac{28R_d}{23\pi}(1-R_s)\left(1-\left(1-\frac{(n,l)}{2}\right)^5\right)\left(1-\left(1-\frac{(n,v)}{2}\right)^5\right)$

$I_{spec}=\frac{\sqrt{(n_x + 1)(n_y + 1)}}{8 \pi (h,l) max((n,l),(n,v))}(n,h)^{n_u \cos^2{\phi} + n_v sin^2\phi}F((h,l))$

На скриншоте ниже приведено изображение тора, освещаемое по этой модели.

Ниже приводится фрагментный шейдер, реализующий данную модель освещения.

//
// Ashikhmin-Shirley fragment shader
//

varying	vec3 l;
varying	vec3 h;
varying vec3 v;
varying	vec3 t;
varying vec3 b;
varying	vec3 n;

uniform float mx, my;
uniform float ks, kd;
uniform float r0, A;

void main (void)
{
    const vec4  diffColor = vec4 ( 1.0, 0.0, 0.0, 1.0 );
    const vec4  specColor = vec4 ( 0.7, 0.7, 0.0, 1.0 );
    const float PI        = 3.1415926;
    const float specPower = 30.0;

    vec3  n2   = normalize ( n );
    vec3  t2   = normalize ( t );
    vec3  b2   = normalize ( b );
    vec3  l2   = normalize ( l );
    vec3  h2   = normalize ( h );
    vec3  v2   = normalize ( v );

    float nv  = max ( 0.0, dot ( n2, v2 ) );
    float nl  = max ( 0.0, dot ( n2, l2 ) );
    float nh  = max ( 0.0, dot ( n2, h2 ) );
    float hl  = max ( 0.0, dot ( h2, l2 ) );
    float t1h = dot ( b2, h );
    float t2h = dot ( t2, h );

                        // calculate diffuse
    float rd = (28.0/(23.0*PI)) * ( 1.0 - pow ( 1.0 - 0.5*nv, 5.0 ) ) * ( 1.0 - pow (1.0 - 0.5*nl, 5.0) );
	
                        // calculate specular
    float B  = pow ( nh, (mx * t1h * t1h + my * t2h * t2h)/(1.0 - nh * nh) );
    float F  = ( r0 + (1.0 - r0) * pow ( 1.0 - hl, 5.0 ) ) / ( hl * max ( nv, nl ) );
    float rs = A * B * F;

    gl_FragColor = nl * ( diffColor * kd * ( 1.0 - ks ) * rd + specColor * ks * rs );
}

Toon shading

Существуют модели освещения, изначально ориентированные на получение изображения, выглядящее как нарисованное человеком. Простейшей подобной моделью является так называемое toon shading. В этой модели освещенность, полученная из одной из стандартных моделей освещения, дискретизируется, приводя к появлению небольшого числа областей с постоянным освещением.

Ниже приводится изображения чайника, построенное таким образом - освещенность от модели Ламберта была модифицирована, как показано на приводимом ниже фрагментном шейдере.

//
// Toon fragment shader
//

varying	vec3 l;
varying vec3 n;

void main (void)
{
    const vec4  diffColor = vec4 ( 0.5, 0.0, 0.0, 1.0 );
    const vec4  specColor = vec4 ( 0.7, 0.7, 0.0, 1.0 );
    const float specPower = 10.0;
    const float edgePower = 3.0;

    vec3  n2   = normalize ( n );
    vec3  l2   = normalize ( l );
    float diff = 0.2 + max ( dot ( n2, l2 ), 0.0 );
    vec4  clr;

    if ( diff < 0.4 )
        clr = diffColor * 0.3;
    else
    if ( diff < 0.7 )
        clr = diffColor ;
    else
        clr = diffColor * 1.3;

    gl_FragColor = clr;
}

Gooch

Еще одной искусственной моделью освещения является модель Ами Гуч. В этой модели диффузная освещенность из модели Ламберта используется для смешивания двух оттенков - "теплого" и "холодного".

$I=lerp\left(C_{cool},C_{warm},\frac{(n,l) + 1}{2}\right)$

//
// Fragment shader for Gooch shading
//

uniform vec3  SurfaceColor;
uniform vec3  WarmColor;
uniform vec3  CoolColor;
uniform float DiffuseWarm;
uniform float DiffuseCool;

varying float NdotL;
varying vec3  reflectVec;
varying vec3  viewVec;

void main (void)
{
    const vec3  surfaceColor = vec3 ( 0.75, 0.75, 0.75 );
    const vec3  warmColor    = vec3 ( 0.6, 0.6, 0.0 );
    const vec3  coolColor    = vec3 ( 0.0, 0.0, 0.6 );
    const float diffuseWarm  = 0.45;
    const float diffuseCool  = 0.45;

    vec3  kCool  = min ( coolColor + diffuseCool * surfaceColor, 1.0 );
    vec3  kWarm  = min ( warmColor + diffuseWarm * surfaceColor, 1.0 );
    vec3  kFinal = mix ( kCool, kWarm, NdotL );
    vec3  r      = normalize ( reflectVec );
    vec3  v      = normalize ( viewVec    );
    float spec   = pow ( max ( dot ( r, v ), 0.0 ), 32.0 );

    gl_FragColor = vec4 ( min ( kFinal + spec, 1.0 ), 1.0 );
}

Rim

Можно слегка изменить стандартную модель освещения, добавив в нее подсветку краев, т.е. мест, где вектор нормали перпендикулярен вектору на наблюдателя.

$I=(1 + b - \max(0,(n,v)))^p$

//
// Rim lighting fragment shader
//
varying	vec3 l;
varying	vec3 h;
varying vec3 v;
varying vec3 n;

void main (void)
{
    const vec4  diffColor = vec4 ( 0.5, 0.0, 0.0, 1.0 );
    const vec4  specColor = vec4 ( 0.7, 0.7, 0.0, 1.0 );
    const float specPower = 30.0;
    const float rimPower  = 8.0;
    const float bias      = 0.3;

    vec3  n2   = normalize ( n );
    vec3  l2   = normalize ( l );
    vec3  h2   = normalize ( h );
    vec3  v2   = normalize ( v );
    vec4  diff = diffColor * max ( dot ( n2, l2 ), 0.0 );
    vec4  spec = specColor * pow ( max ( dot ( n2, h2 ), 0.0 ), specPower );
    float rim  = pow ( 1.0 + bias - max ( dot ( n2, v2 ), 0.0 ), rimPower );

    gl_FragColor = diff + rim * vec4 ( 0.5, 0.0, 0.2, 1.0 ) + spec * specColor;
}

Subsurface scattering

Можно слегка модифицировать одну из обычных моделей освещения для имитации эффекта подповерхностного рассеивания (subsurface scattering).

uniform float matThickness;  
uniform vec3  extinction;
uniform vec4  lightColor;  
uniform vec4  baseColor;  
uniform vec4  specColor;  
uniform float specPower;  
uniform float rimScalar;  

varying vec3 n, eyeVec, lightVec, vertPos, lightPos;  
   
float halfLambert(in vec3 vect1, in vec3 vect2 )  
{  
     return dot ( vect1, vect2 ) * 0.5 + 2.0;
}  
   
float blinnPhongSpecular(in vec3 normalVec, in vec3 lightVec, in float specPower)  
{  
     vec3 halfAngle = normalize ( normalVec + lightVec ); 
	 
     return pow ( clamp ( 0.0, 1.0, dot ( normalVec, halfAngle ) ), specPower );
}  
   
void main()  
{  
    float	attenuation = 1.0 / distance ( lightPos, vertPos );
    vec3	e        = normalize(eyeVec);  
    vec3	l        = normalize(lightVec);  
    vec3	nn       = normalize(n);  
    vec4	ln       = baseColor * attenuation * halfLambert ( l, nn );
	float   inFactor = max ( 0.0, dot ( -nn, l ) ) + halfLambert ( -e, l );	 
    vec3	indirect = vec3 ( matThickness * inFactor * attenuation ) * extinction; 
    vec3 rim = vec3 ( 1.0 - max ( 0.0, dot ( nn, e )));  
	 
    rim *= rim;  
    rim *= max ( 0.0, dot ( nn, l ) ) * specColor.rgb;  
   
    vec4 color = ln + vec4 ( indirect, 1.0 );  
	 
    color.rgb += (rim * rimScalar * attenuation);  
    color.rgb += vec3( blinnPhongSpecular ( nn, l, specPower ) * attenuation * specColor * 0.3);
   
    gl_FragColor = color;
}

Bidirectional Lighting

Кроме модели Гуч есть еще несколько простых моделей освещения, использующие интерполяцию между двумя или тремя цветами. Одной из таких моделей является модель bidirectional lighting. Ее можно рассматривать как освещение сразу с двух противоположных сторон сторон источниками с разными цветами:

$I=C_0\max({0,(n,l)}) + C_2\max({0,(-n,l)})$

//
// Bi-directional lighting fragment shader
//

varying	vec3 l;
varying vec3 n;

void main (void)
{
    const vec4 color0 = vec4 ( 0.5, 0.0, 0.0, 1.0 );
    const vec4 color2 = vec4 ( 0.5, 0.5, 0.0, 1.0 );

    vec3 n2   = normalize ( n );
    vec3 l2   = normalize ( l );
    vec4 diff = color0 * max ( dot ( n2, l2 ), 0.0 ) + color2 * max ( dot ( n2, -l2 ), 0.0 );

    gl_FragColor = diff;
}

Hemispheric Lighting

Эта модель подобно модели Гуч использует диффузную освещенность для линейной интерполяции цветов.

$I=lerp(C_2,C_0,\frac{(n,l) + 1}{2})$

//
// Hemispheric lighting fragment shader
//

varying	vec3 l;
varying vec3 n;

void main (void)
{
    const vec4 color0 = vec4 ( 0.5, 0.0, 0.0, 1.0 );
    const vec4 color2 = vec4 ( 0.5, 0.5, 0.0, 1.0 );

    vec3 n2   = normalize ( n );
    vec3 l2   = normalize ( l );
    vec4 diff = mix ( color2, color0,  ( dot ( n2, l2 ) + 1.0 ) * 0.5 );

    gl_FragColor = diff;
}

Trilight Model

Данная модель является обобщением двух предыдущим, более подробно о чей можно прочесть в здесь.

$I=C_0\max({0,(n,l)}) + C_1 (1-|(n,l)|) + C_2\max({0,(-n,l)})$

//
// Trilight lighting fragment shader
//

varying	vec3 l;
varying vec3 n;

void main (void)
{
    const vec4 color0 = vec4 ( 0.5, 0.0, 0.0, 1.0 );
    const vec4 color1 = vec4 ( 0.5, 0.5, 0.0, 1.0 );
    const vec4 color2 = vec4 ( 0.5, 0.5, 0.5, 1.0 );

    vec3 n2   = normalize ( n );
    vec3 l2   = normalize ( l );
    vec4 diff = color0 * max ( dot ( n2, l2 ), 0.0 ) + color1 * ( 1.0 - abs ( dot ( n2, l2)) ) + color2 * max ( dot ( -n2, l2), 0.0 );

   gl_FragColor = diff;
}

Lommel-Seeliger model

$I=C_0\frac{\max(0,(n,l))}{\max(0,(n,l))+\max(0,(n,v))}$

//
// Lommel-Seeliger fragment shader
//

varying	vec3 l;
varying	vec3 h;
varying vec3 v;
varying vec3 n;

void main (void)
{
	const vec4	diffColor = vec4 ( 0.5, 0.0, 0.0, 1.0 );
	const vec4	specColor = vec4 ( 0.7, 0.7, 0.0, 1.0 );
	const float	specPower = 30.0;

	vec3	n2   = normalize ( n );
	vec3	l2   = normalize ( l );
	vec3	v2   = normalize ( v );
	float	a    = max ( 0.0, dot ( n2, l2 ) );
	float	b    = max ( 0.0, dot ( n2, v2 ) );

	gl_FragColor = diffColor * a / (a + b);
}

Strauss model

//
// Strauss fragment shader
//

uniform	float	smooth;
uniform	float	metal;
uniform	float	transp;
uniform	float	r0;

varying	vec3 l;
varying	vec3 h;
varying vec3 v;
varying vec3 n;

float	fresnel ( float x, float kf )
{
	float	dx  = x - kf;
	float	d1 = 1.0 - kf;
	float	kf2 = kf * kf;
	
	return (1.0 / (dx * dx) - 1.0 / kf2) / (1.0 / (d1 * d1) - 1.0 / kf2 );
	//return 1.0;
}

float	shadow ( float x, float ks )
{
	float	dx  = x - ks;
	float	d1 = 1.0 - ks;
	float	ks2 = ks * ks;
	
	//return (1.0 / (dx * dx) - 1.0 / ks2) / (1.0 / (d1 * d1) - 1.0 / ks2 );
	return 1.0;
}

void main (void)
{
	const vec4	diffColor = vec4 ( 1.0, 0.0, 0.0, 1.0 );
	const vec4	specColor = vec4 ( 1.0, 1.0, 0.0, 1.0 );
	const float	k  = 0.1;
	const float kf = 1.12;
	const float ks = 1.01;
	
	vec3	n2 = normalize ( n );
	vec3	l2 = normalize ( l );
	vec3	v2 = normalize ( v );
	vec3	h2 = reflect   ( l2, n2 );
	float 	nl = dot( n2, l2 );
	float 	nv = dot( n2, v2 );
	float	hv = dot( h2, v2 );
	float	f  = fresnel( nl, kf );
	float	s3 = smooth * smooth * smooth;
 
			// diffuse term
	float	d    = ( 1.0 - metal * smooth );
	float	Rd   = ( 1.0 - s3 ) * ( 1.0 - transp );
	vec4	diff = nl * d * Rd * diffColor;
 
			// inputs into the specular term
	float	r       = (1.0 - transp) - Rd;
	float	j       = f * shadow ( nl, ks ) * shadow ( nv, ks );
	float	reflect = min ( 1.0, r + j * ( r + k ) );
	vec4	C1      = vec4 ( 1.0 );
	vec4 	Cs      = C1 + metal * (1.0 - f) * (diffColor - C1); 
	vec4	spec    = Cs * reflect;

	spec *= pow ( -hv, 3.0 / (1.0 - smooth) );
 
			// composite the final result, ensuring
	diff = max ( vec4 ( 0.0 ), diff );
	spec = max ( vec4 ( 0.0 ), spec );

	gl_FragColor = diff + spec*specColor;
}

По этой ссылке можно скачать весь исходный код к этой статье. Также доступны для скачивания откомпилированные версии для M$ Windows, Linux и Mac OS X.

Используются технологии uCoz