Что такое Reversed z и как его использовать в OpenGL и Vulkan

Давайте вспомним для начала как в OpenGL происходит преобразования координат при рендеринге. После выполнения перспективного деления мы получаем так называемые NDC-координаты (Normalized Device Coordinates), видимая область в них образует куб \( [-1,1]^3 \) в трехмерном пространстве.

При рендеринге координаты вершин обычно проходят целую цепочку преобразований, изображенную на рис. 1.

Рис. 1. Цепочка преобразования координат в OpenGL

Изначально координаты задаются в пространстве модели (model space), потом при помощи модельной матрицы (model matrix) они переводятся в единую мировую систему координат (world space). У нас может несколько копий одного и того же объекта с одними и теми же модельными координатами, но у каждой копии своя модельная матрица и при переводе в мировые координаты мы получаем разные координаты. Фактически мировые координаты - это единые координаты всей сцены со всеми объектами в ней. Эти координаты не зависят от положения и ориентации камеры.

Далее мы преобразовываем мировые координаты в систему координат наблюдателя/камеры (view space) при помощи видовой матрицы. После этого мы применяем матрицу проектирования, переводящую координаты камеры в пространство отсечения (clip space). Видимая область сцены в этих координатах задается набором следующих неравенств:

\[ \begin{matrix} \begin{aligned} & -w_{clip} \leq x_{clip} \leq w_{clip} \\ & -w_{clip} \leq y_{clip} \leq w_{clip} \\ & -w_{clip} \leq z_{clip} \leq w_{clip} \\ \end{aligned} \end{matrix} \]

После этого применяется перспективное деление, т.е. координаты делятся на \( w_{clip} \). В результате мы получаем так называемые нормализованные координаты устройства (NDC, Normalized Device Coordinates). В OpenGL они изменяются в \( [-1,1]^3 \).

Стандартная матрица перспективного проектирования в OpenGL имеет следующий вид:

\[ Р = \begin{pmatrix} a & 0 & 0 & 0 \\ 0 & b & 0 & 0 \\ 0 & 0 & c & d \\ 0 & 0 & -1 & 0 \end{pmatrix} \]

Коэффициенты a и b определяются ближней и дальней плоскостями отсечения \( z_{near} \) и \( z_{far} \). Ниже приводятся формулы для коэффициентов этой матрицы

\[ \begin{matrix} \begin{aligned} & a = \frac{ 1 }{ aspect \cdot \tan \frac{fov}{2} } \\ & b = \frac{ 1 }{ \tan \frac{fov}{2} } \\ & c = -\frac{ z_{far} + z_{near} }{ z_{far} - z_{near} } \\ & d = -\frac{ 2 z_{near} z_{far} }{ z_{far} - z_{nar} } \\ & aspect = \frac{ width }{ height } \end{aligned} \end{matrix} \]

В результате мы получаем

\[ z_{NDC} = -c - \frac {d}{z_{clip} } \]

И в буфер глубины будет на замом деле записано именно \( z_{NDC} \) перемасштабированное в \( [0,1] \). Т.е. на самом деле в буфер глубины записывается не z-координата в системе координат камеры, а функция от \( \frac{1}{z} \).

То, что мы записываем в буфер глубины, это не z, а функция \( \frac{1}{z} \) связано с тем, что именно \( \frac{1}{z} \) линейно изменяется в координатах экрана (пикселах). Это позволяет использовать для получения записываемого в буфер глубины значения обычную билинейную интерполяцию.

Как работает такой буфер глубины понятно, но возникает важный (и обычно не рассматриваемый) вопрос - а что у нас происходит с точностью ? В буфере глубины обычно хранятся значения, представленные 16, 24 или 32 битами и вопрос в том, как именно распределяются эти биты по всему диапазону от \( z_{near} \) до \( z_{far} \).

Давайте начнем с самого простого случая - у нас приведенная глубина изменяется от 0 до 1 (как в Direct3D и Vulkan) и лога хранится в виде числа с фиксированной точкой. Тогда если разбить весь диапазон изменения глубины \( [z_{near}, z_{far}] \) на равные части и отобразить точки разбиения на графике мы получим следующую картинку:

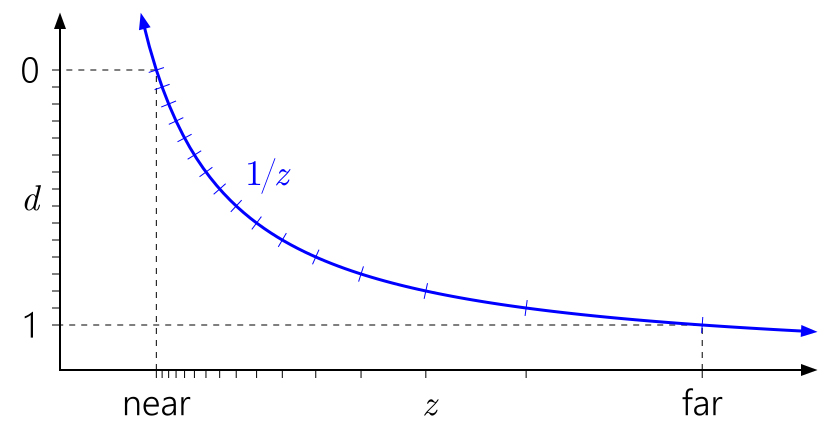
Рис 2. Распределение точности для глубины из \( [0,1] \) Видно, что получающееся распределение точности очень плохое - наибольшая точность у нас получается в окрестности \( z = z_{near} \), а наименьшая - в окрестности \( z = z_{far} \) (рис 2). Понятно, что это крайне нежелательное (и весьма неожиданное) поведение. P> Что происходит в классическом OpenGL и что будет если мы для повышения точности перейдем к хранению глубины в виде значений с плавающей точкой. В этом случае картинка слегка меняется - мы получаем следующий график. Видно что вся точность сосредоточена где-то в середине и что у ближней плоскости отсечения, что у дальней точность очень низкая.

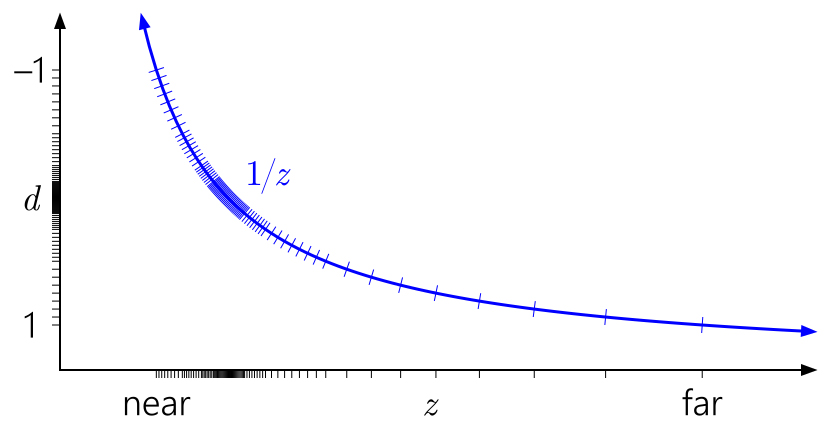
Рис 3. Точность для 1/z (с сайта nvidia)

В OpenGL 4.5 вошло расширение ARB_clip_control, которое позволяет при отсечении использовать не \(z=-1 \), а \( z = 0 \).

При помощи функции glClipControl (вводимой этим расширением), мы можем управлять отсечением невидимой геометрии. Если параметр depth равен GL_NEGATIVE_ONE_TO_ONE, то для отсечения по z будет использоваться уравнение \( -w_c \leq z_c \). В случае, когда depth равен GL_ZERO_TO_ONE, то для отсечения по z будет использоваться неравенство \( z_c >= 0 \).

void glClipControl ( GLenum origin, GLenum depth );

При помощи параметра origin мы можем управлять направлением оси Oy - доступны два значения - GL_LOWER_LEFT и GL_UPPER_LEFT. Обратите внимание, что при определении того, является ли треугольник лицевым или нет используется площадь треугольника со знаком и она зависит от направления оси Oy.

По умолчанию используются значения (GL_LOWER_LEFT, GL_NEGATIVE_ONE_TO_ONE).

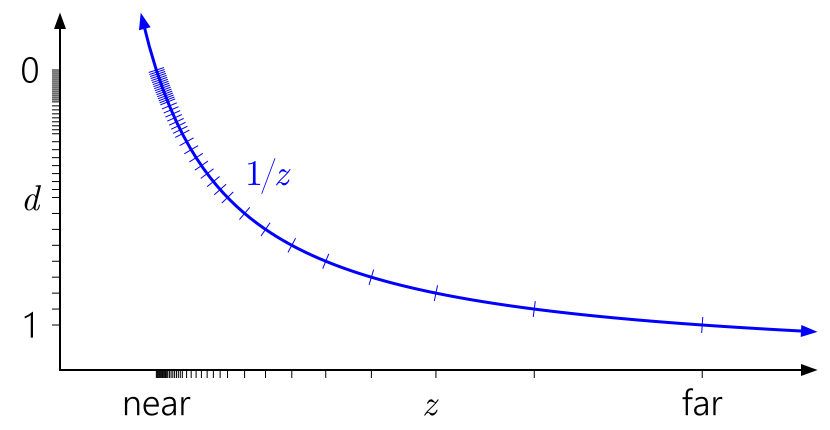
Рис 4. Что будет если использовать для z диапазон [0,1]

Видно, что если мы просто перейдем в OpenGL от диапазона [-1,1] для z к [0,1], то сильно лучше не стало - точность в окрестности \( z = z_{far} \) по прежнему крайне низкая. Это значит что вдали от камеры мы можем столкнуться с так называемым z-fighting, когда нам не хватает точности буфера глубины и возникает хорошо заметные визуальные артефакты.

Что произойдет, если мы "перевернем" z - так что, записываемое в буфер значение \( d = 0 \) будет соответствовать дальней плоскости отсечения, а \( d = 1 \) - ближней ? С точки зрения работы буфера глубины не изменится ничего, надо только изменить правило сравнения в тесте глубины с GL_LESS на GL_GREATER и изменить значение, которым мы будем инициализировать буфер глубины.

А вот с точностью произойдут огромные изменения - мы получим в результате почти равномерное распределение точности по всему диапазону \( [z_{near}, z_{far}] \). И при этом резкого падения точности при \( z = z_{far} \) уже не будет, как не будет его и при \( z = z_{near} \).

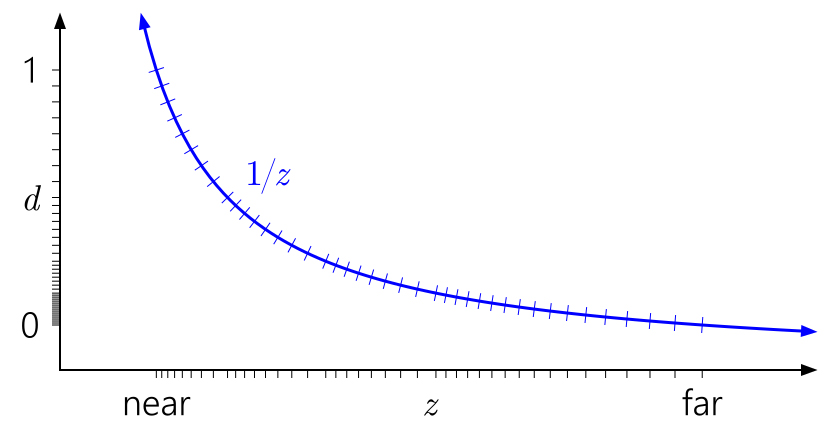
Рис 5. Распределение точности при reversed-z

Вот такой подход и получил название reversed-z и смысл его применения заключается в том, чтобы получить более равномерное распределение точности буфера глубины по всей сцене.

Использование reversed-z в OpenGL

Для перехода к reversed-z в OpenGL нам нужно выполнить несколько шагов. Во-первых при помощи команды glClipControl нам нужно перейти к диапазону \([0,1]\) при отсечении геометрии.

glClipControl ( GL_LOWER_LEFT, GL_ZERO_TO_ONE );

Во-вторых, для использования reversed-z нужно использовать формат буфера глубины с плавающей точкой, т.е. GL_DEPTH_COMPONENT32F.

// we need floating point z-buffer
fb.create             ( getWidth (), getHeight (), 0 );
fb.bind               ();
fb.attachColorTexture ( fb.createColorTexture () );
fb.attachDepthTexture ( fb.createDepthTexture ( GL_DEPTH_COMPONENT, GL_DEPTH_COMPONENT32F,
                        GL_CLAMP_TO_BORDER, FrameBuffer::filterNearest ) );
        
if ( !fb.isOk () )
    exit ( "Error with fb\n" );
            
fb.unbind ();

Поскольку теперь дальней плоскости соответствует значение 0, то нам нужно изменить значение, которым мы будем очищать буфер глубины.

glClearDepth ( 0.0f );

Также нам нужно изменить операцию сравнения, используемую в тесте глубины на GL_GREATER.

glDepthFunc ( GL_GREATER );

Также нам нужно изменить нашу матрицу проектирования. Фактически нам нужно выполнить два дополнительных преобразования над z - сперва из \( [-1,1] \) в \( [0,1] \) и потом перевернуть его, заменив z на 1-z. Пусть наша матрица проектирования имеет вид

\[ Р = \begin{pmatrix} a & 0 & 0 & 0 \\ 0 & b & 0 & 0 \\ 0 & 0 & c & d \\ 0 & 0 & -1 & 0 \end{pmatrix} \]

Здесь использованы следующие обозначения \[ \begin{matrix} \begin{aligned} & a = \frac{f}{a} \\ & b = f \\ & c = \frac{ z_{near} + z_{far} }{ z_{near} - z_{far} } \\ & d = \frac{ 2 z_{near} z_{far} }{ z_{near} - z_{far} } \end{aligned} \end{matrix} \]

Тогда нам нужно умножить эту матрицу на произведение следующих матриц

\[ \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & -1 & 1 \\ 0 & 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1/2 & 1/2 \\ 0 & 0 & 0 & 1 \end{pmatrix} \]

В результате этого умножения мы получаем матрицу того же вида, но два элемента изменились:

\[ \begin{matrix} \begin{aligned} & c' = -\frac{ z_{near} }{ z_{near} - z_{far} } \\ & d' = -\frac{ z_{near} z_{far} }{ z_{near} - z_{far} } \end{aligned} \end{matrix} \]

На практике обычно рассматривают случай бесконечно удаленно дальней плоскости. Для этого достаточно в приведенных выше формулах выполнить предельный переход при \( z_{far} \rightarrow \infty \). В результате мы получаем следующую матрицу:

\begin{pmatrix} a & 0 & 0 & 0 \\ 0 & b & 0 & 0 \\ 0 & 0 & 0 & z_{near} \\ 0 & 0 & -1 & 0 \end{pmatrix}

Ниже приводятся функции, строящие соответствующие матрицы проектирования с использованием библиотеки GLM.

// create reversed-z projection
glm::mat4 perspectiveReversed ( float fovy, float n, float f )
{
    float aspect = getAspect ();
    float b      = 1.0f / tan ( fovy );
    float a      = b / aspect;
    float c      = n / (f - n);
    float d      = (n * f) / (f - n);

    return glm:: mat4 (
        a,    0.0f, 0.0f,  0.0f, 
        0.0f, b,    0.0f,  0.0f, 
        0.0f, 0.0f, c,    -1.0f, 
        0.0f, 0.0f, d,     0.0f );
}
    
    // create reversed-z projection with infinite zFar
glm::mat4 perspectiveReversedInf ( float fovy, float n  )
{
    float aspect = getAspect ();
    float b      = 1.0f / tan ( fovy );
    float a      = b / aspect;
    float c      = 0.0f;            // n / (f - n)       -> 0
    float d      = n;               // (n * f) / (f - n) -> n

    return glm:: mat4 (
        a,    0.0f, 0.0f,  0.0f, 
        0.0f, b,    0.0f,  0.0f, 
        0.0f, 0.0f, c,    -1.0f, 
        0.0f, 0.0f, d,     0.0f );
}

Если собрать все это вместе, то можно получить следующий код на С++ для осуществления рендеринга на OpenGL с использованием reversed-z.

#include    "GlutRotateWindow.h"
#include    "Program.h"
#include    "BasicMesh.h"
#include    "Texture.h"
#include    "Framebuffer.h"

class   TestWindow : public GlutRotateWindow
{
    Program         program;
    Texture         tex;
    FrameBuffer     fb;
    glm::vec3       eye;
    glm::vec3       light;
    float           fovY  = 60.0f;
    float           zNear = 0.1f;
    BasicMesh     * mesh  = nullptr;

public:
    TestWindow () : GlutRotateWindow ( 200, 100, 900, 900, "Reversed-Z" )
    {
            // we need floating point z-buffer
        fb.create             ( getWidth (), getHeight (), 0 );
        fb.bind               ();
        fb.attachColorTexture ( fb.createColorTexture () );
        fb.attachDepthTexture ( fb.createDepthTexture ( GL_DEPTH_COMPONENT, GL_DEPTH_COMPONENT32F, GL_CLAMP_TO_BORDER, FrameBuffer::filterNearest ) );
        
        if ( !fb.isOk () )
            exit ( "Error with fb\n" );
            
        fb.unbind ();

        if ( !tex.load2D ( "../../Textures/oak.jpg" ) )
            exit ( "Error loading decal texture\n" );
    
        if ( !program.loadProgram ( "lighting.glsl" ) )
            exit ( "Error building program: %s\n", program.getLog ().c_str () );
        
        mesh = loadMesh ( "../../Models/teapot.3ds", 0.1f );
        
        if ( mesh == nullptr )
            exit ( "Error loading mesh" );
        
        eye   = glm::vec3 ( 4, 4, 4 );
        light = glm::vec3 ( 7, 7, 7 );
        
        program.bind       ();
        program.setTexture ( "decalMap", 0 );
        tex.bind           ( 0 );

        setupReversedZ ();
    }

    void redisplay () override
    {
        fb.bind ();
        
        glm::mat4   mv = getRotation  ();
        glm::mat3   nm = normalMatrix ( mv );
        
        glClear ( GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT );

        program.setUniformMatrix ( "mv",  mv );
        program.setUniformMatrix ( "nm",  nm );

        mesh -> render ();
        
        fb.unbind ();
        
            // copy color buffer from fb
        glBlitNamedFramebuffer ( fb.getId (), 0, 
                                 0, 0, getWidth () - 1, getHeight () - 1,
                                 0, 0, getWidth () - 1, getHeight () - 1,
                                 GL_COLOR_BUFFER_BIT, GL_NEAREST );
    }

    void reshape ( int w, int h ) override
    {
        GlutRotateWindow::reshape ( w, h );
        
        glm::mat4 proj = perspectiveReversedInf ( fovY, zNear );
        
        program.setUniformMatrix ( "proj",  proj  );
        program.setUniformVector ( "eye",   eye   );
        program.setUniformVector ( "light", light );
    }

    void    idle () override
    {
        float   angle  = 4 * getTime ();

        light.x = 8*cos ( angle );
        light.y = 8*sin ( 1.4 * angle );
        light.z = 8 + 0.5 * sin ( angle / 3 );

        program.setUniformVector ( "eye",   eye   );
        program.setUniformVector ( "light", light );

        glutPostRedisplay ();
    }

    void    setupReversedZ ()
    {
        glClipControl ( GL_LOWER_LEFT, GL_ZERO_TO_ONE );
        glClearDepth  ( 0.0f );
        glDepthFunc   ( GL_GREATER );
    }

        // create reversed-z projection
    glm::mat4 perspectiveReversed ( float fovy, float n, float f )
    {
        float aspect = getAspect ();
        float b      = 1.0f / tan ( fovy );
        float a      = b / aspect;
        float c      = n / (f - n);
        float d      = (n * f) / (f - n);

        return glm:: mat4 (
            a,    0.0f, 0.0f,  0.0f, 
            0.0f, b,    0.0f,  0.0f, 
            0.0f, 0.0f, c,    -1.0f, 
            0.0f, 0.0f, d,     0.0f );
    }
    
        // create reversed-z projection with infinite zFar
    glm::mat4 perspectiveReversedInf ( float fovy, float n  )
    {
        float aspect = getAspect ();
        float b      = 1.0f / tan ( fovy );
        float a      = b / aspect;
        float c      = 0.0f;            // n / (f - n)       -> 0
        float d      = n;               // (n * f) / (f - n) -> n

        return glm:: mat4 (
            a,    0.0f, 0.0f,  0.0f, 
            0.0f, b,    0.0f,  0.0f, 
            0.0f, 0.0f, c,    -1.0f, 
            0.0f, 0.0f, d,     0.0f );
    }
};

int main ( int argc, char * argv [] )
{
    GlutWindow::init ( argc, argv );
    
    TestWindow  win;
    
    return GlutWindow::run ();
}

Использование reversed-z в Vulkan

Давайте теперь рассмотрим как сделать то же самое в Vulkan. В Vulkan z изменяется на \( [0,1] \), поэтому ряд шагов, которые мы делали ранее, уже не нужны. Но матрицу проектирования нам все-таки придется изменить - для этого ее достаточно домножить на матрицу, "переворачивающую" z, т.е. на

\[ \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & -1 & 1 \\ 0 & 0 & 0 & 1 \end{pmatrix} \]

Классическая матрица перспективного проектирования в Vulkan выглядит следующим образом:

\[ Р_V = \begin{pmatrix} a & 0 & 0 & 0 \\ 0 & b & 0 & 0 \\ 0 & 0 & c & d \\ 0 & 0 & -1 & 0 \end{pmatrix} \]

Здесь использованы следующие обозначения \[ \begin{matrix} \begin{aligned} & a = \frac{f}{a} \\ & b = f \\ & c = \frac{ z_{far} }{ z_{far} - z_{near} } \\ & d = -\frac{ z_{near} \cdot z_{far} }{ z_{far} - z_{near} } \end{aligned} \end{matrix} \]

В результате умножения мы получим следующую матрицу

\[ Р_V = \begin{pmatrix} a & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1-c & -d \\ 0 & 0 & -1 & 0 \end{pmatrix} \]

Для получения бесконечной дальней плоскости отсечения, делаем предельный переход \( z_{far} \rightarrow \infty \). В результате получаем

\[ \begin{matrix} \begin{aligned} & c \rightarrow 1 - 1 = 0 \\ & d \rightarrow -z_{near} \end{aligned} \end{matrix} \]

Ниже приводится функция на С++, создающая такую матрицу

glm::mat4 perspectiveProjection ( float fovY, float aspectWbyH, float zNear )
{
    float f = 1.0f / tanf ( fovY / 2.0f );
    return glm::mat4 (
        f / aspectWbyH, 0.0f, 0.0f,  0.0f,
        0.0f,           f,    0.0f,  0.0f,
        0.0f,           0.0f, 0.0f,  1.0f,
        0.0f,           0.0f, zNear, 0.0f );
}

Исходный код для примера на OpenGL можно скачать здесь. Пример на Vulkan доступен в репозитории на github - https://github.com/steps3d/vulkan-with-classes.git.

Восстановление трехмерных координат по значениям из буфера глубины

Есть еще одно изменение в коде, которое нужно будет внести, если вы используете reversed-z. Если потом в шейдере читается значение из буфера глубины и по нему восстанавливаются трехмерные координаты, то при reversed-z нужно внести изменения в код.

Давайте рассмотрим reverse-z в OpenGL. Координаты в системе координат камеры преобразуются в координаты в пространстве отсечение следующим образом (нас интересуют только z и w, поэтому рассмотрим нижнюю правую подматрицу).

\[ \begin{pmatrix} z_{clip} \\ w_{clip} \end{pmatrix} = \begin{pmatrix} c & d \\ -1 & 0 \end{pmatrix} \cdot \begin{pmatrix} z_{eye} \\ w_{eye} \end{pmatrix} \]

После этого выполняется перспективное деление и мы получаем нормализованные координаты устройства.

\[ z_{NDC} = \frac {z_{eye}}{w_{eye}} = \frac {c \cdot z_{eye} + d}{ -z_{eye} } = -c - \frac {d}{z_{eye}} \]

В классическом OpenGL мы получаем значение от -1 до 1 и для записи в буфер глубины его надо привести в \( [0,1] \).

\[ D = \frac {1 + z_{NDC}}{2} = -\frac{1}{2} \left ( c + \frac {d}{z_{eye}} \right ) \]

У нас z изменяется на \( [0,1] \) поэтому это преобразование не нужно и \( D = z_{NDC} \). В случае бесконечно удаленной дальней плоскости мы получаем

\[ D = z_{NDC} = -\frac {z_{near}}{z_{eye}} \]

Отсюда мы получаем формулу для восстановления \( z_{eye} \) по значению \( D \) из буфера глубины:

\[ z_{eye} = - \frac {z_{near}}{D} \]

Расчет остальных координат ( x и y ) все остается также как и всегда.

Полезные ссылки

Reversed-Z in OpenGL

Reverse Z (and why it's so awesome)

Depth Precision Visualized

Reverse Depth Buffer in OpenGL

Reversed-Z Rendering in OpenGL

Reverse Z Cheatsheet

https://github.com/Zswop/ReversedZ