Visibility buffer

Давайте вспомним, почему появилось отложенное освещение (deferred shading). Это на самом деле связано с тем, что сильно выросла как геометрическая сложность сцены (т.е. число треугольников N и overdraw), так и сложность по освещению (число источников света, L). При этом если мы используем традиционную модель рендеринга (forward shading), то итоговая сложность оказывается равна произведению геометрической сложности на сложность по освещению (NL). Т.е. получающаяся сложность рендеринга стала просто слишком большой.

Отложенное освещение это фактически просто способ отделить геометрическую сложность сцены от сложности по освещению - вместо их произведения мы получаем их сумму. Для этого весь рендеринг сцены разбивается на два прохода. На первом проходе задействована только геометрическая сложность - в ходе этого прохода из геометрии строится так называемый G-буфер (или геометрический буфер). И вся сложность по геометрии влияет только на первый проход, после этого прохода мы вообще не работаем с геометрией, только с освещением.

В результате этого прохода мы получаем готовый G-буфер, т.е. набор текстур, содержащих для каждого пиксела экрана всю информацию, необходимую для его освещения. В эту информацию обычно входят 3D-координаты (на самом деле достаточно только z-координаты), цвет (альбедо), неровность, металличность и т.п. Важно заметить, что тем самым мы для каждого пиксела храним довольно большой объем информации, что приводит к большой нагрузке на шину памяти.

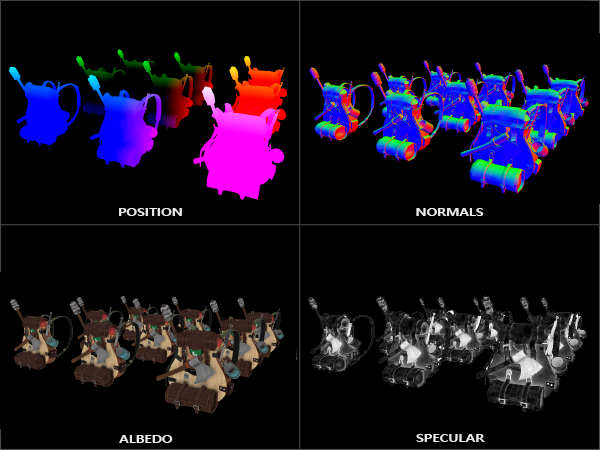
Рис 1. Пример готового G-буфера с координатами (POSITION), нормалями (NORMALS), цветом (ALBEDO) и бликовостью (SPECULAR).

После первого прохода следует второй проход. Его задача - по подготовленному G-буферу построить изображение сцены с наложенной освещенностью. При этом для этого прохода геометрия сцены вообще не нужна - только G-буфер. Тем самым мы рассчитываем освещенность только для видимых фрагментов сцены и на этом проходе задействована только сложность сцены по освещению.

Тем самым мы отделили геометрию от освещения и считаем его только для видимых фрагментов сцены, итоговая сложность рендеринга будет N+L. Однако осталось еще место, где это разбиение на ортогональные операции не было выполнено. На первом проходе мы для каждого фрагмента для построения G-буфера должны прочесть из текстур довольно большой объем данных.

При этом мы читаем его вообще для всех получающихся при растеризации фрагментов, не важно будут ли они впоследствии видны или нет. Это приводит к большой нагрузке на шину памяти, причем чем выше overdraw, тем выше будет эта нагрузка. Поэтому хотелось бы и здесь провести отделение и читать данные из текстур только для видимых фрагментов (а не для всех подряд).

Именно такой подход и был предложен в ставшей классической работе C. Burns and W. Hunt - The visibility buffer: A cache-friendly approach to deferred shading. Предложенный ими подход заключается в том, что вся геометрия рендерится не в G-буфер (требующий многочисленных чтений из текстур), а в специальный буфер, получивший название visibility buffer. В нем для каждого пиксела экрана хранится просто беззнаковое 32-битовое целое число. Оно задает какой именно треугольник сцены виден в данном пикселе. Обычно 32 бита разбивается на две группы битов - в одном хранится id меша/кластера, а в другой - id треугольника внутри него.

uint id = (meshId << TRIANGLE_BITS) | triangleId;

Тем самым на первом проходе нам нужен только буфер глубины (чтобы определять видимость) и этот visibility buffer, содержащий информацию о том, какой именно треугольник в результате будет виден в данном пикселе. Никакого чтения из текстур вообще не требуется, используется простейший фрагментный шейдер и занимающий мало памяти visibility buffer.

В оригинальной работе было предложено сразу по visibility buffer считать итоговую освещенность. Однако позже в Nanite и ряде других движков пришли к выводу, что выгодно использовать трехпроходную схему. На втором проходе мы по visibility buffer строим G-буфер, а на третьем рассчитываем освещенность как при обычном отложенном освещении. Это связано с тем, что данные из G-буфера часто бывают нужны для различных эффектов.

Однако кроме отделения определения видимости от чтения свойств материалов из текстур есть еще один момент, который также говорит в пользу visibility buffer. Каждый раз, когда мы в фрагментном шейдере читаем из текстуры при помощи функции texture, то скрыто от нас происходит определение слоя (или слоев) mipmap-пирамиды, из которого мы будем в действительности читать. Для этого на самом деле на этапе растеризации каждый треугольник переводится не в отдельные фрагменты, а в блоки (квады, quad) 2x2 фрагментов и именно эти блоки идут далее.

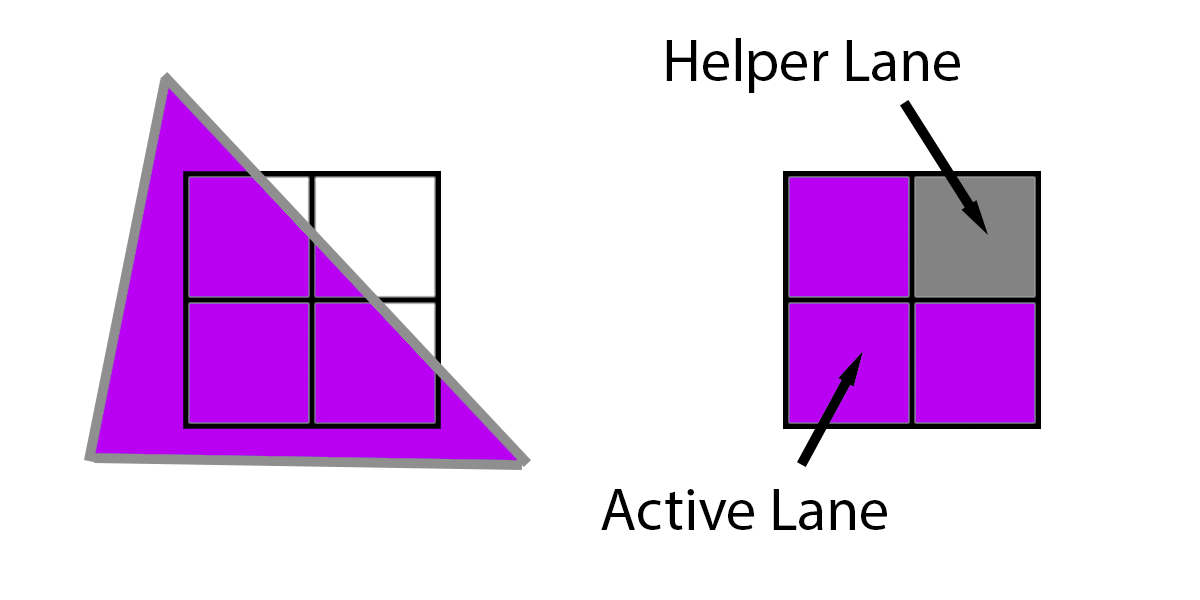
Рис 2. Блок 2x2 фрагментов, получаемый при растеризации треугольника, и добавление фиктивного фрагмента (helper lane) для получения полного блока.

Как видно из рис. 2 может (и на самом деле регулярно) возникнуть ситуация, когда для получения полного квада 2x2 нужно к реальным фрагментам, получаемым при растеризации (active lane), добавить вспомогательные (helper lane). Начиная с OpenGL 4.5 в фрагментном шейдере доступна специальная логическая (bool) переменная gl_HelperInvocation. С ее помощью шейдер может узнать является ли данный обрабатываемый фрагмент настоящим (значение переменной равно false) или это фиктивный фрагмент для получения полного квада (значение переменной равно true).

Тогда, когда фрагментный шейдер обрабатывает команду texture(myMap, uv), то фактически одно ядро GPU выполняет код для всех четырех фрагментов квада и у него есть значения uv для всех его четырех фрагментов. Поэтому можно вычислить разности по вертикали и горизонтали между текстурными координатами uv фрагментов квада. Эти разности фактически являются частными производными текстурных координат по экранным.

Эти производные можно явно получить для любой переменой в GLSL через встроенные функции dFdx и dFdy. И именно через эти производные и считается уровень в mipmap-пирамиде, как показано на следующем фрагменте коде.

vec2   dx  = dFdx ( uv );
vec2   dy  = dFdy ( uv );
float  lod = log2 ( max ( length ( dx ), length ( dy ) ) );

Легко видно, что вспомогательные фрагменты добавляются только на границе треугольника (рис 3). Если треугольник большой, то доля добавленных фрагментов будет невелика. Но если у нас много маленьких треугольников, то как показано на рис. 4 у нас число добавленных фрагментов легко может превысить количество регулярных фрагментов. Есть термин quad utilization, обозначающий какую долю от квада составляют настоящие фрагменты. Чем этот параметр ближе к 100%, тем лучше.

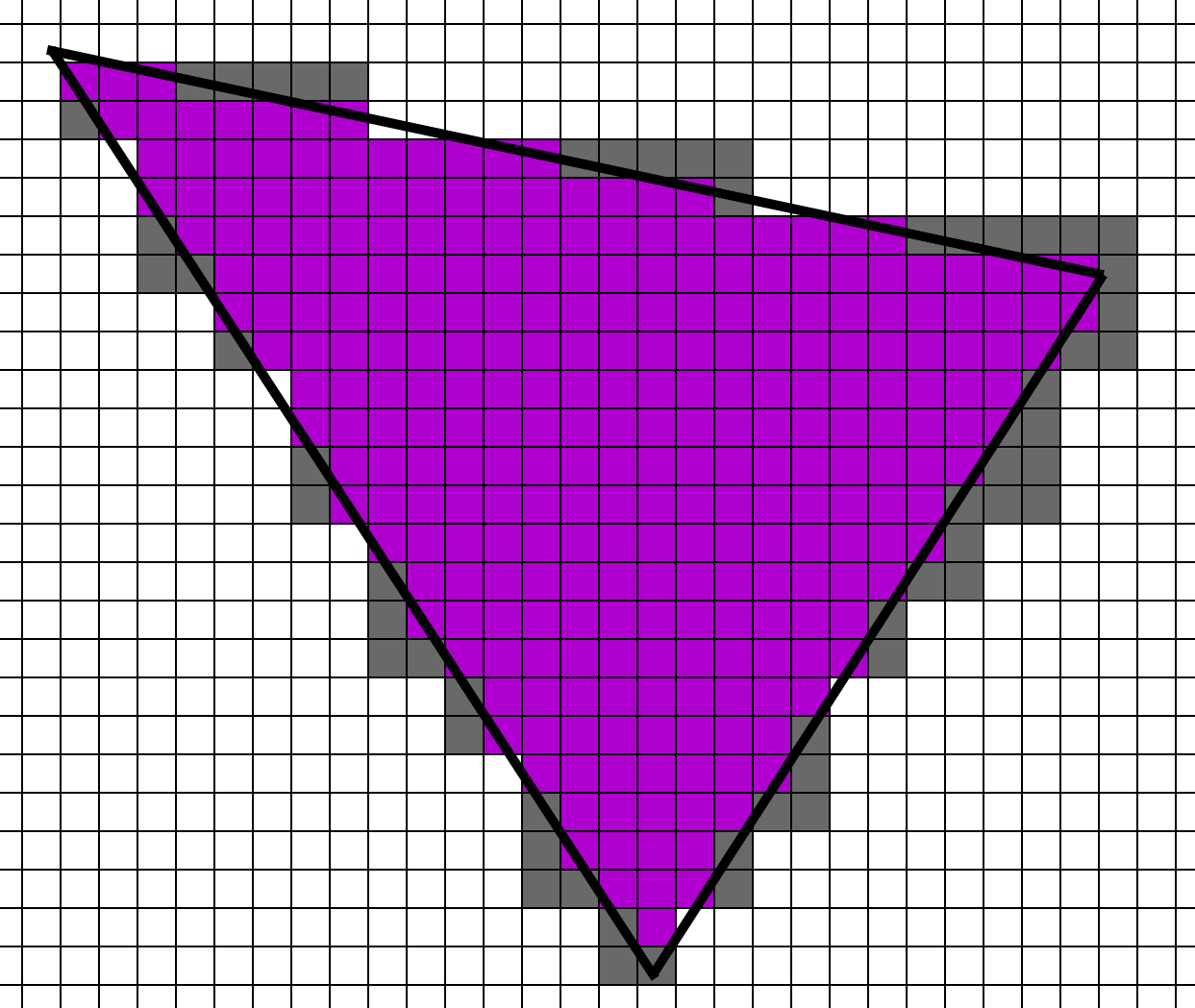
Рис 3. Настоящие и добавленные фрагменты при рендеринге треугольника.

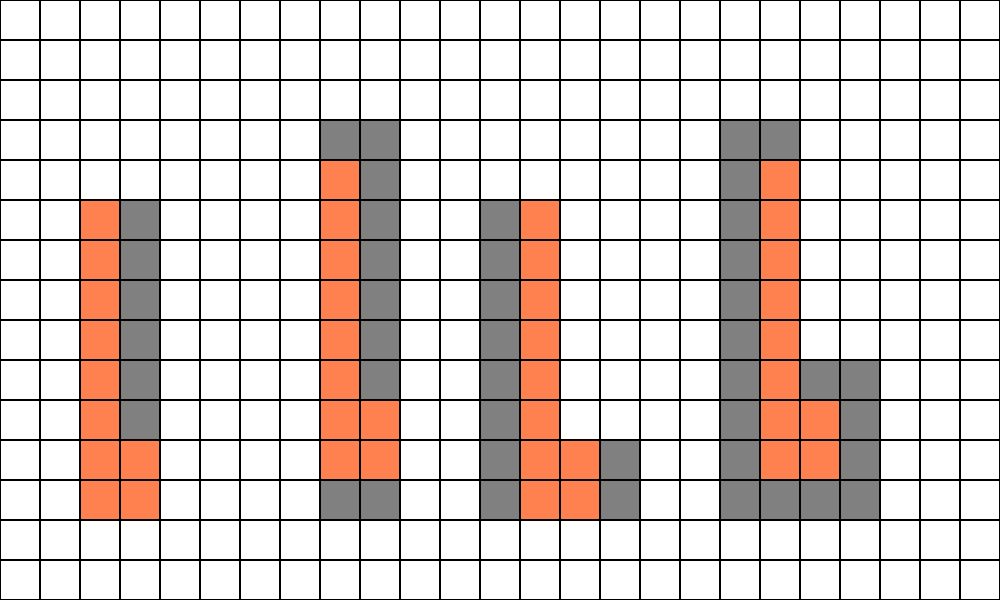
Рис 4. Добавленные фрагменты при рендеринга маленьких треугольников.

Но в случае маленьких треугольников (т.е. высокодетализированных мешей) у нас сильно растет число дополнительных фрагментов, а значит растет цена рендеринга - ведь они также обрабатываются ядрами GPU. При этом чем сложнее шейдер, тем дороже нам это будет обходится. И в случае visibility buffer так как у нас крайне простой фрагментный шейдер, то плата за дополнительные фрагменты будет минимальной. А следующие два прохода от геометрии не зависят и дополнительных фрагментов у нас скорее всего просто не будет. А вот для традиционного или отложенного освещения дополнительные фрагменты создают заметную нагрузку.

Общая схема работы метода

Первый проход крайне прост - мы просто выводим всю геометрию, выводя в фрагментном шейдере построенный уникальный id для треугольника. Обычно он просто строится из gl_DrawID и gl_PrimitiveID. Весь рендеринг производится в однокомпонентную (GL_RED_INTEGER) текстуру, использующей беззнаковые 32-битовые целые значения для каждого пиксела (внутренний формат GL_R32UI).

#version 460 core

layout(location = 0) in vec4 pos;

uniform mat4 mv;
uniform mat4 proj;

flat out uint drawID;       // integer varying (out) must be flat

void main(void)
{
    drawID      = uint ( gl_DrawID );
    gl_Position = proj * mv * vec4 ( pos.xyz, 1.0 );
}

#version 460 core

flat in  uint drawID;

layout ( location = 0 ) out uint triangle;      // triangle id

void main ()
{
    triangle = 1 + gl_PrimitiveID + (drawID << 16);     // 0 mean empty
}

Второй проход оказывается заметно сложнее (фактически он оказывается самым сложным из всех трех проходов). Зная координаты текущего пиксела (например как gl_FragCoord.xy) и разрешение экрана мы можем выпустить луч из камеры через центр пиксела (рис 5).

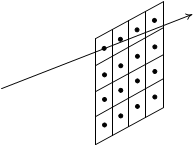
Рис 5. Построение луча для тексела из visibility buffer

Далее, зная треугольник, мы извлекаем все его вершины (просто прочитав их из SSBO). По координатам вершин \( v_0 \), \( v_1 \) и \( v_2 \) мы можем легко найти пересечение луча с этим треугольником. Это пересечение находится в виде барицентрических координат точки пересечения. Зная эти координаты мы можем найти значения всех атрибутов вершин в данной точке.

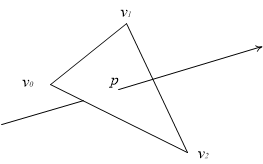
Рис 6. Нахождение пересечения луча и треугольника

Но на самом деле не все так просто. Во первых, мы не можем просто использовать обычную билинейную интерполяцию для атрибутов. Это связано с тем, что обычно используется перспективное проецирование. Поэтому используемая схема интерполяции должна быть perspective correct.

Это обычно реализуется следующим образом. Пусть у нас есть некоторый вершинный атрибут a. Тогда если w это четвертая компонента однородных координат, то величины 1/w и a/w изменяются линейно (в NDC- или экранных координатах). Поэтому для их определения можно использовать обычную линейную интерполяцию (через барицентрические координаты). После того, как в точке пересечения мы нашли 1/w и a/w через линейную интерполяцию, мы можем найти a как частное этих двух значений.

\[ a = \frac{a/w}{1/w} \]

Второй момент связан с тем, что мы не можем для чтения из текстур использовать обычную функцию texture. Это происходит потому, что если мы в фрагментном шейдере вызываем эту функцию, то используются частные производные текстурных координат по экранным координатам для определения уровня в mipmap-пирамиде.

Эти производные находятся как разности между соседними фрагментами - фрагменты всегда обрабатываются блоками 2x2, это позволяет строить разности для определения производных. Но это работает только при выводе оригинальной геометрии. А у нас второй проход может быть либо вычислительным шейдером, либо фрагментным шейдером, выполняемым для полноэкранного прямоугольника. Т.е. разностных производных у нас или вообще нет или они неверные.

Поэтому нам нужно не просто проинтерполировать атрибуты с учетом перспективы, нам нужно еще найти градиент текстурных координат. Зная градиент, мы можем читать свойства поверхности из текстур через textureGrad.

Нахождение пересечения луча с треугольником

Пусть у нас есть треугольник с вершинами \( v_0 \), \( v_1 \) и \( v_2 \). Тогда любую точку этого треугольника можно записать при помощи барицентрических координат. Обычно барицентрические координаты обозначают как u, v, и w. Но у нас будут также использоваться однородные координаты и там будет четвертая компонента этих координат, которая тоже обычно обозначается как w. Поэтому чтобы не возникало путаницы, я оставлю w однородным координатам, а барицентрические координаты буду обозначать как \( \lambda_0 \), \( \lambda_1 \) и \( \lambda_2 \) (следуя статье по DAIS, см ссылки в конце). Тогда произвольная точка треугольника p может быть записана через свои барицентрические координаты следующим образом:

\[ p = \lambda_0 v_0 + \lambda_1 v_1 + \lambda_2 v_2 \]

Тем самым задачу нахождения пересечения луча (с началом в точке \( p_0 \) и направлением d), можно свести к следующему векторному уравнению (относительно \( t, \lambda_0, \lambda_1 \) )

\[ p_0 + l t = \lambda_0 v_0 + \lambda_1 v_1 + (1 - \lambda_0 - \lambda_1) v_2 \]

Введем следующие обозначения:

\[ e_1 = v_1 - v_0 \] \[ e_2 = v_2 - v_0 \] \[ s = p_0 - v_0 \]

Тогда решение этой системы уравнений можно записать по правилу Крамера следующим образом:

\[ \begin{pmatrix}t\\u\\v \end{pmatrix} = \frac{1}{det(-l,e_1,e_2)} \begin{pmatrix} det(s,e_1,e_2)\\det(-l,s,e_2)\\det(-l,e_1,s) \end{pmatrix} \]

Здесь через det(a,b,c) обозначен определитель матрицы 3x3, столбцами которой являются вектора a, b, и c. Используя векторное произведение этот определитель можно переписать следующим образом:

\[ det(a,b,c) = (-[a,c], b) \]

Тогда приведенную выше формулу для решения системы уравнений можно будет записать в следующем виде:

\[ \begin{pmatrix}t\\u\\v \end{pmatrix} = \frac{1}{(x,e_1)} \begin{pmatrix} (l,e_1)\\(x,s)\\(y,l) \end{pmatrix} \]

\[ x = [l, e_2] \] \[ y = [s, e_1] \]

В общем случае, найдя решение этой системы, необходимо убедиться, что решение удовлетворяет условию \( \lambda_0, \lambda_1, 1 - \lambda_0 - \lambda_1 \in [0,1] \). Если оно не выполнено, то соответствующая точка не принадлежит треугольнику, т.е. нет пересечения луча с треугольником. Но в нашем случае мы точно знаем, что пересечение есть, поэтому эти проверки можно опустить. В результате мы приходим к следующему коду на GLSL:

vec3 rayTriangleIntersection ( vec3 p0, vec3 p1, vec3 p2, vec3 origin, vec3 dir )
{
    vec3  e1     = p1 - p0;
    vec3  e2     = p2 - p0;
    vec3  pvec   = cross ( dir, e2 );
    float det    = dot   ( e1, pvec );
    float invDet = 1.0 / det;
    vec3  tvec   = origin - p0;
    vec3  qvec   = cross ( tvec, e1 );
    float u      = dot   ( tvec, pvec ) * invDet;
    float v      = dot   ( dir, qvec  ) * invDet;
    float w      = 1.0 - v - u;
    
    return vec3 ( u, v, w );
}

На самом деле можно искать барицентрические координаты не в 3D как показано выше, а уже в 2D, т.е. после проектирования при помощи однородных координат. Давайте рассмотрим как можно найти барицентрические координаты зная однородные координаты вершин треугольника \( v_0, v_1 \) и \( v_2 \). Для начала найдем по ним NDC координаты проекций вершин на экран:

\[ p_i = v_{i,xy} / v_{i,w} \]

Теперь пусть p(x,y) это некоторая точка, заданная также своими NDC-координатами x и y. По аналогии с ранее рассмотренным алгоритмом нахождения пересечения луча и треугольника в 3D, можно написать разложение точки p по барицентрическим координатам треугольника следующим образом:

\[ \lambda_0(x,y) = \frac{(y_1 - y_2)(x - x_2) + (x_2 - x_1)(y - y_2)}{D} \tag{1} \] \[ \lambda_1(x,y) = \frac{(y_2 - y_0)(x - x_2) + (x_0 - x_2)(y - y_2)}{D} \tag{2} \] \[ \lambda_2(x,y) = 1 - \lambda_0 - \lambda_1 \] \[ D = det(p_2 - p_1, p_0 - p_2) = (y_1 - y_2)(x_0 - x_2) + (x_2 - x_1)(y_0 - y_2) \]

Также удобно ввести вектор \( \lambda = (\lambda_0, \lambda_1, \lambda_2) \). Из этих формул мы можем легко найти частные производные барицентрических координат по NDC-координатам x и y.

\[ \frac{\partial \lambda_0}{\partial x} = \frac{y_1 - y_2}{D}, \frac{\partial \lambda_1}{\partial x} = \frac{y_2 - y_0}{D}, \frac{\partial \lambda_2}{\partial x} = \frac{y_0 - y_1}{D} \tag{3} \] \[ \frac{\partial \lambda_0}{\partial y} = \frac{x_2 - y_1}{D}, \frac{\partial \lambda_1}{\partial y} = \frac{x_0 - x_2}{D}, \frac{\partial \lambda_2}{\partial y} = \frac{x_1 - x_0}{D} \tag{4} \] \[ \lambda_x = \left ( \frac{\partial \lambda_0}{\partial x}, \frac{\partial \lambda_1}{\partial x}, \frac{\partial \lambda_2}{\partial x} \right ) \] \[ \lambda_y = \left ( \frac{\partial \lambda_0}{\partial y}, \frac{\partial \lambda_1}{\partial y}, \frac{\partial \lambda_2}{\partial y} \right ) \]

Это можно легко реализовать следующим фрагментом кода на GLSL:

vec3    w    = vec3 ( v0.w, v1.w, v2.w );
vec3    invW = 1.0 / w;

    // compute NDC coordinates of triangle vertices
vec2    p0 = v0.xy * invW.x;
vec2    p1 = v1.xy * invW.y;
vec2    p2 = v2.xy * invW.z;

    // compute 1/D
float   invD = 1.0 / determinant ( mat2 ( p2 - p1, p0 - p1 ) );

    // compute barycentrics lambda of NDC point (x,y)
vec3    lambda;

lambda.x = (( p1.y - p2.y )*( x - p2.x ) + ( p2.x - p1.x ) * ( y - p2.y )) * invD;
lambda.y = (( p2.y - p0.y )*( x - p2.x ) + ( p0.x - p2.x ) * ( y - p2.y )) * invD;
lambda.z = 1.0 - lambda.x - lambda.y;

    // compute gradient
vec3    lx = vec3 ( p1.y - p2.y, p2.y - p0.y, p0.y - p1.y ) * invD;
vec3    ly = vec3 ( p2.x - p1.x, p0.x - p2.x, p1.x - p0.x ) * invD;

Обратите внимание, что барицентрические координаты в 3D отличаются от барицентрических координат в 2D из-за перспективных искажений. Поэтому нахождение производных по x и y не так просто, как может показаться. Фактически барицентрические координаты в 2D соответствуют следующим равенствам:

\[ \lambda_0 \frac{1}{w_0} \begin{pmatrix} x_0\\y_0 \end{pmatrix} + \lambda_1 \frac{1}{w_1} \begin{pmatrix} x_1\\y_1 \end{pmatrix} + \lambda_2 \frac{1}{w_2} \begin{pmatrix} x_2\\y_2 \end{pmatrix} = \frac{1}{w} \begin{pmatrix} x\\y \end{pmatrix} \]

Как видно покоординатная запись для 2D и 3D отличается множителем \( w_i \), а значит отличаются и барицентрические координаты \( \lambda \). На следующем рисунке показано, как середина отрезка при перспективном проектировании переходит не в середину проекции.

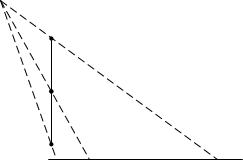
Рис 7. Смещение середины отрезка при перспективном проецировании.

Нахождение градиента текстурных координат

Давайте теперь рассмотрим, как можно найти производные некоторого атрибута, заданного в вершинах. Пусть у нас есть некоторый скалярный вершинный атрибут a. Мы легко можем выписать производную по x и y от линейно изменяющейся a/w:

\[ \frac{\partial (a/w)}{\partial x} = \frac{\partial \lambda_0}{\partial x} \frac{a_0}{w_0} + \frac{\partial \lambda_1}{\partial x} \frac{a_1}{w_1} + \frac{\partial \lambda_2}{\partial x} \frac{a_2}{w_2} = \left (\lambda_x, \frac{a}{w} \right) \tag{5} \] \[ \frac{\partial (a/w)}{\partial y} = \frac{\partial \lambda_0}{\partial y} \frac{a_0}{w_0} + \frac{\partial \lambda_1}{\partial y} \frac{a_1}{w_1} + \frac{\partial \lambda_2}{\partial y} \frac{a_2}{w_2} = \left (\lambda_y, \frac{a}{w} \right) \tag{6} \] \[ a = (a_0, a_1, a_2) \] \[ w = (w_0, w_1, w_2) \]

Также легко можно найти частные производные от 1/w:

\[ \frac{\partial (1/w)}{\partial x} = \frac{\partial \lambda_0}{\partial x} \frac{1}{w_0} + \frac{\partial \lambda_1}{\partial x} \frac{1}{w_1} + \frac{\partial \lambda_2}{\partial x} \frac{1}{w_2} = \left ( \lambda_x, \frac{1}{w} \right) \] \[ \frac{\partial (1/w)}{\partial y} = \frac{\partial \lambda_0}{\partial y} \frac{1}{w_0} + \frac{\partial \lambda_1}{\partial y} \frac{1}{w_1} + \frac{\partial \lambda_2}{\partial y} \frac{1}{w_2} = \left ( \lambda_y, \frac{1}{w} \right) \]

Используя выведенные производные \( \frac{\partial (1/w)}{\partial x} \) и \( \frac{\partial (1/w)}{\partial y} \) мы можем найти значение однородной координаты w в произвольной точке p(x,y) путем линейной интерполяции значения 1/w, которое линейно изменяется в NDC-координатах. А раз оно линейно изменяется, значит ее градиент постоянен и не изменяется. Отсюда следует, что для нахождения значения w(x,y) в произвольной точке p(x,y) можно использовать следующую формулу

\[ \frac{1}{w(x,y)} = \frac{1}{w_0} + (x - x_0) \frac{\partial (1/w)}{\partial x} + (y - y_0) \frac{\partial (1/w)}{\partial y} = \frac{1}{w_0} + (x-x_0) \left ( \lambda_x, \frac{1}{w} \right ) + (y-y_0) \left ( \lambda_y, \frac{1}{w} \right ) \tag{7} \]

Отсюда можно вывести формулы для частных производных a как производных частного (здесь величины a и w без индекса обозначают значения в текущей точке).

\[ \frac{\partial a}{\partial x} = \frac{\partial}{\partial x} \left( \frac{a/w}{1/w} \right) = w^2 \left ( {\frac{\partial (a/w)}{\partial x} \frac{1}{w} - \frac{\partial (1/w)}{\partial x} \frac{a}{w} } \right ) = w^2 \left ( \frac{\partial \lambda_0}{\partial x} \frac{a_0}{w_0} + \frac{\partial \lambda_1}{\partial x} \frac{a_1}{w_1} + \frac{\partial \lambda_2}{\partial x} \frac{a_2}{w_2} \right ) \frac{1}{w} - \left ( \frac{\partial \lambda_0}{\partial x} \frac{1}{w_0} + \frac{\partial \lambda_1}{\partial x} \frac{1}{w_1} + \frac{\partial \lambda_2}{\partial x} \frac{1}{w_2} \right ) \frac{a}{w} \]

Давайте введем кроме NDC-координат x и y еще и экранные координаты X и Y (в пикселах). Тогда справедливы следующие формулы (через W и H обозначен размер экрана в пикселах):

\[ X = \frac{x + 1}{2} W \] \[ Y = \frac{y + 1}{2} H \]

Тогда если у нас есть некоторая величина (функция) f, то мы можем выразить ее производные по экранным координатам через градиент по x и y:

\[ \frac{\partial f}{\partial X} = \frac{\partial f}{\partial x} \frac{\partial x}{\partial X} = \frac { \frac{\partial f}{\partial x} } { \frac{\partial X}{\partial x} } = \frac{\partial f}{\partial x} \frac {2}{W} \] \[ \frac{\partial f}{\partial Y} = \frac{\partial f}{\partial y} \frac{\partial y}{\partial Y} = \frac { \frac{\partial f}{\partial y} } { \frac{\partial Y}{\partial y} } = \frac{\partial f}{\partial y} \frac {2}{H} \]

Теперь давайте на основе уже найденных значений найдем w(x+1,y). Мы можем выразить это значение через w(x,y) и градиент 1/w (который равен константе и который мы нашли ранее (7)). Мы опять работаем с линейно изменяющейся 1/w.

\[ \frac{1}{w(x + 1, y )} = \frac{1}{w(x,y)} + \frac{\partial \lambda_0}{\partial x} \frac{1}{w_0} + \frac{\partial \lambda_1}{\partial x} \frac{1}{w_1} + \frac{\partial \lambda_2}{\partial x} \frac{1}{w_2} = \frac{1}{w(x,y)} + 1 \cdot \left ( \lambda_x, \frac{1}{w} \right ) \]

Мы можем использовать формулы (5)-(6) для нахождения градиента линейно изменяющегося значения \( \lambda/w \). Давайте вместо вершинного атрибута a рассмотрим величину \( \lambda_0 \). Тогда для нее мы получим вектор значений в вершинах \( ( 1, 0, 0 ) \). Поэтому в этом случае формулу (5) можно переписать в следующем виде (здесь через \( \lambda_{x,x} \) обозначена x-компонента от \( \lambda_x \)):

\[ \frac{\partial (\lambda_0/w) }{\partial x} = \lambda_{x,x} \cdot \frac{1}{w_0} \]

В результате мы можем для производных \( \lambda/w \) записать следующие формулы (здесь через * обозначено поэлементное умножение векторов):

\[ \frac{\partial (\lambda/w) }{\partial x} = \lambda_x * \frac{1}{w} \tag{8} \] \[ \frac{\partial (\lambda/w) }{\partial y} = \lambda_y * \frac{1}{w} \tag{9} \]

Из этих формул мы можем найти значение \( \lambda/w \) в соседних с (x,y) точках.

\[ \frac{\lambda(x+1,y)}{w(x+1,y)} = \frac{\lambda(x,y)}{w(x,y)} + \lambda_x * \frac{1}{w} \]

Мы можем использовать уже найденное значение для для w(x+1,y), в результате чего мы приходим к следующей формуле (аналогичная формула может быть записана и для \( \lambda(x,y+1) \) ):

\[ \lambda(x+1, y) = w(x+1,y) \left( \frac{\lambda(x,y)}{w(x,y)} + \lambda_x * \frac{1}{w} \right) \]

Тогда мы можем найти точное значение \( \frac{\partial \lambda}{\partial x} \) через конечную разность (как это на самом деле делает GPU при растеризации):

\[ \frac{\partial \lambda}{\partial x}(x, y) = \lambda(x+1,y) - \lambda(x, y) \] \[ \frac{\partial \lambda}{\partial н}(x, y) = \lambda(x,y+1) - \lambda(x, y) \]

Теперь давайте рассмотрим как это можно реализовать в виде кода. На вход у нас поступают однородные координаты вершин треугольника v₀, v₁ и v₂. Также нам понадобится координаты текущего фрагмента в NDC (т.е. от -1 до 1) и размер окна в пикселах winSize (мы можем получить его при помощи функции textureSize для входного visibility buffer).

vec3    w    = vec3 ( v0.w, v1.w, v2.w );
vec3    invW = 1.0 / w;

    // compute NDC coordinates of triangle vertices
vec2    p0 = v0.xy * invW.x;
vec2    p1 = v1.xy * invW.y;
vec2    p2 = v2.xy * invW.z;

    // compute barycentrics lambda of NDC point (x,y)
vec3    lambda;

lambda.x = (( p1.y - p2.y )*( x - p2.x ) + ( p2.x - p1.x ) * ( y - p2.y )) * invD;
lambda.y = (( p2.y - p0.y )*( x - p2.x ) + ( p0.x - p2.x ) * ( y - p2.y )) * invD;
lambda.z = 1.0 - lambda.x - lambda.y;

    // compute 1/D
float   invD = 1.0 / determinant ( mat2 ( p2 - p1, p0 - p1 ) );

    // compute gradient
vec3    lx = vec3 ( p1.y - p2.y, p2.y - p0.y, p0.y - p1.y ) * invD;
vec3    ly = vec3 ( p2.x - p1.x, p0.x - p2.x, p1.x - p0.x ) * invD;

    // compute w at (x,y) by linearly interpolating 1/w
vec2    delta = vec2 ( x, y ) - p0;

    // compute gradient of 1/w
float   diwdx  = lx.x * invW.x + lx.y * invW.y + lx.z * invW.z;
float   diwdy  = ly.x * invW.x + ly.y * invW.y + ly.z * invW.z;

    // now lerp 1/w
float   iwp = invW.x + delta.x * diwdx + delta.y * diwdy;
float   wp  = 1.0 / iwp;

    // convert to pixels
dldx *= 2.0 / winSize.x;
dldy *= 2.0 / winSize.y;

    // compute w(x+1,y), w (x,y+1)
float   wx1 = 1.0 / ( iwp + dot ( lx, invW ) );
float   wy1 = 1.0 / ( iwp + dot ( ly, invW ) );

    // now compute lambda(x+1,y) and lambda(x,y+1)
vec3    lx1 = wx1 * ( lambda * iwp + lx * invW );
vec3    ly1 = wy1 * ( lambda * iwp + ly * invW );

    // and now get final lambda gradients
vec3    ddx = (lx1 - lambda) * invW;
vec3    ddy = (ly1 - lambda) * invW;

Еще один способ расчета градиента

Приведенный выше способ дает корректный градиент, но математически довольно сложен. Есть другой (альтернативный) способ нахождения градиента барицентрических координат, которой с одной стороны, гораздо проще, но с другой стороны требует больше арифметических инструкций.

Сам подход очень прост - давайте мы выпустим не один луч, а сразу три луча. Они будут соответствовать точкам (x,y), (x+1,y) и (x,y+1). Для каждого из них мы находим пересечение луча с треугольником (для двух последних лучей точка пересечения может уже не лежать внутри треугольника, но это не важно). Обратите внимание, что здесь мы ищем пересечение (и барицентрические координаты) в 3D. А найдя три набора \( \lambda \) мы находим градиент через разности:

\[ \frac{\partial \lambda}{\partial x} = \lambda ( x+1,y) - \lambda ( x, y) \] \[ \frac{\partial \lambda}{\partial y} = \lambda ( x,y+1) - \lambda ( x, y) \]

Ниже приводится простейший вариант кода, реализующего данный подход для расчета градиента.

// Calculate ray differentials for a point in world-space
// - v0,v1,v2 -> world space coordinates of the triangle currently visible on the pixel
// - ndc -> 2D NDC position of current pixel, range [-1, 1]
// - rayOrigin -> camera position
void CalcRayBary(vec3 pt0, vec3 pt1, vec3 pt2, vec2 pixelNdc, vec3 rayOrigin, 
        mat4 viewInv, mat4 projInv, vec2 twoOverScreenSize,
        out vec3 lambda, out vec3 ddx, out vec3 ddy )
{
      // On the near plane, calculate the NDC of two nearby pixels in X and Y directions
    vec3 ndcPos = vec3 ( ndc, 0.0 );
    vec3 ndcDx  = vec3 ( ndc + vec2 ( 2.0 / winSize.x, 0 ), 0.0 );
    vec3 ndcDy  = vec3 ( ndc - vec2 ( 0, 2.0 / winSize.y ), 0.0 );
 
      // Inverse projection transform into view space
    vec4 viewPos = projInv * vec4 ( ndcPos, 1.0 );
    vec4 viewDx  = projInv * vec4 ( ndcDx,  1.0 );
    vec4 viewDy  = projInv * vec4 ( ndcDy,  1.0 );
 
      // Inverse view transform into world space
      // By setting homogeneous coordinate W to 0, 
      // this directly generates ray directions
    vec3 rayDir   = normalize ( (viewInv * vec4(viewPos.xyz, 0)).xyz);
    vec3 rayDirDx = normalize ( (viewInv * vec4(viewDx.xyz,  0)).xyz);
    vec3 rayDirDy = normalize ( (viewInv * vec4(viewDy.xyz,  0)).xyz);
 
      // Ray-triangle intersection for barycentric coordinates
    vec3 lambdaDx = rayTriangleIntersection ( v0, v1, v2, rayOrigin, rayDirDx );
    vec3 lambdaDy = rayTriangleIntersection ( v0, v1, v2, rayOrigin, rayDirDy );

    lambda = rayTriangleIntersection ( v0, v1, v2, rayOrigin, rayDir );
 
      // Derivatives
    ddx    = lambdaDx - lambda;
    ddy    = lambdaDy - lambda;
}

Интерполяция атрибутов вершин

Как уже отмечалось ранее, в случае перспективного проецирования мы уже не можем использовать линейную интерполяцию значений в вершинах треугольника для получения значений внутри него (в экранных или NDC-координатах). То есть если у нас есть точка внутри треугольника, заданная своими барицентрическими координатами и есть значения некоторого атрибута в вершинах \( a_0 \), \( a_1 \) и \( a_2 \), то нельзя просто считать, что \( a = a_0 \lambda_0 + a_1 \lambda_1 + a_2 \lambda_2 = (a, \lambda) \).

Вместо этого, мы должны использовать тот факт, что \( a/w \) и \( 1/w \) линейно изменяются в NDC (и, следовательно) экранных координатах. Тогда мы можем выразить значение нашего атрибута в произвольной точке, как частное:

\[ a = \frac{a_0 \lambda_0 \frac{1}{w_0} + a_1 \lambda_1 \frac{1}{w_1} + a_2 \lambda_2 \frac{1}{w_2} }{ \lambda_0 \frac{1}{w_0} + \lambda_1 \frac{1}{w_1} + \lambda_2 \frac{1}{w_2} } = \frac{(a, \frac{\lambda}{w} ) } {(\lambda, \frac{1}{w} )} \]

Для интерполяции двухмерного атрибута можно использовать следующую функцию.

vec2 interpolate2D ( in vec3 lambda, in vec3 invW, vec2 a, vec2 b, vec2 c ) 
{
    float   den = dot ( lambda, invW );
    return (a * lambda.x * invW.x + b * lambda.y * invW.y + c * lambda.z * invW.z) / den;
}

Реализация и проверки

Ниже приводится фрагментный шейдер на GLSL, который по visibility buffer вычисляет корректные текстурные координаты точки. В зависимости от значения параметра mode выводятся барицентрические координаты точки, настоящие текстурные координаты, рассчитанные текстурные координаты и разница между рассчитанными и точными.

В приводимой реализации есть один тонкий момент, связанный с тем, что пример делается на OpenGL, на нем режим выравнивания scalar не поддерживается, только std140 и std430. А для этих режимов выравнивание структуры происходит по размеру наибольшего элемента структуры. Таким образом, пусть у нас есть структура Vertex, как показано ниже.

struct Vertex
{
    vec4 pos;
    vec2 tex;
};

Тогда при размещение массива структур Vertex внутри буфера, каждый элемент будет выравниваться исходя из размера vec4, т.е. по 16 байтам. Таким образом сама структура будет занимать в массиве 32 байта, оставляя 8 байт неиспользуемыми. Это не согласуется с выравниванием аналогичной структуры в С++.

Есть две способа как обойти это не создавая "дырки" в памяти (и не используя режим выравнивания scalar из Vulkan). Первый - это мы разносим эти атрибуты по разным буферам - в одном будут только значения типа vec4, а в другом - только типа vec2. Для большого числа атрибутов это довольно неудобный подход.

Второй подход (который и используется в приводимых далее примерах) - это описать каждую вершину как массив из float. Минус подхода - мы должны уметь сами собирать нужные атрибуты из элементов массива, для чего в приводимом ниже коде вводятся специальные функции. Но обратите внимание, что в случае использования Visibility buffer имеет смысл отдельно разнести координаты вершин и все остальные атрибуты по двум разным вершинным буферам - на первом проходе нам будут нужны только координаты вершин. Все остальные атрибуты понадобятся уже на этапе построения G-буфера.

Ниже приводится исходный код фрагментного шейдера для примера vb-2. Он показывает как строить барицентрические координаты и с их использованием как правильно восстанавливать текстурные координаты в произвольной точке треугольника. В этом примере при помощи клавиш + и - можно переключать режим показа - что именно будет видно - барицентрические координаты, настоящие текстурные координаты или рассчитанные текстурные координаты. Для того, чтобы можно было произвести сравнение помимо visibility buffer строится также вспомогательные буфер в котором будут храниться настоящие текстурные координаты для каждой точки.

#version 460 core

struct  Vertex
{
    float   f [6];
};

layout ( std430, binding = 0 ) buffer Vertices
{
    float   f [];
};

uniform usampler2D visMap;
uniform sampler2D  testMap;

uniform mat4 mv;
uniform mat4 proj;
uniform int  mode;

in  vec2  tex;
in  vec2  viewRay;
out vec4  color;

vec4    getPos ( int triangle, int no )
{
    int index = 3 * 6 * triangle + no * 6;
    
    return vec4 ( f[index + 0], f[index + 1], f[index + 2], f[index + 3] );
}

vec2    getTex ( int triangle, int no )
{
    int index = 3 * 6 * triangle + no * 6;
    
    return vec2 ( f[index + 4], f[index + 5] );
}

    // intersect ray (origin, dir) with triangle v0, v1, v2
    // return bary-coordinates, no checks are performed
vec3 rayTriangleIntersection ( vec3 v0, vec3 v1, vec3 v2, vec3 origin, vec3 dir )
{
    vec3  e1     = v1 - v0;
    vec3  e2     = v2 - v0;
    vec3  pvec   = cross ( dir, e2 );
    float det    = dot   ( e1, pvec );
    float invDet = 1.0 / det;
    vec3  tvec   = origin - v0;
    vec3  qvec   = cross ( tvec, e1 );
    float u      = dot   ( tvec, pvec ) * invDet;
    float v      = dot   ( dir, qvec  ) * invDet;
    
    return vec3 ( u, v, 1.0 - u - v );
}

void main(void)
{
    vec2    ndc = 2*tex - vec2 ( 1.0 );     // convert to NDC
    uint    id = texture ( visMap, tex ).x;
    
    if ( id < 1 )
        discard;
        
    id--;
    
    mat4    m  = proj * mv;
    vec4    v0 = m * getPos ( 0, 0 );
    vec4    v1 = m * getPos ( 0, 1 );
    vec4    v2 = m * getPos ( 0, 2 );

    vec3    w    = vec3 ( v0.w, v1.w, v2.w );
    vec3    invW = 1.0 / w;

        // compute NDC coordinates of triangle vertices
    vec2    p0 = v0.xy * invW.x;
    vec2    p1 = v1.xy * invW.y;
    vec2    p2 = v2.xy * invW.z;

        // compute 1/D
    float   invD = 1.0 / determinant ( mat2 ( p2 - p1, p0 - p2 ) );

        // compute barycentrics lambda of NDC point (x,y)
    vec3    lambda;

    lambda.x = (( p1.y - p2.y )*( ndc.x - p2.x ) + ( p2.x - p1.x ) * ( ndc.y - p2.y )) * invD;
    lambda.y = (( p2.y - p0.y )*( ndc.x - p2.x ) + ( p0.x - p2.x ) * ( ndc.y - p2.y )) * invD;
    lambda.z = 1.0 - lambda.x - lambda.y;

        // now do perspective-correct texture coordinates interpolation
    vec2    tx0 = getTex ( 0, 0 );
    vec2    tx1 = getTex ( 0, 1 );
    vec2    tx2 = getTex ( 0, 2 );
        
    float   den = dot ( lambda, invW );
    vec2    uv  = (tx0 * lambda.x * invW.x + tx1 * lambda.y * invW.y + tx2 * lambda.z * invW.z) / den;
    
    if ( mode == 0 )        // show baricentrics
        color = vec4 ( lambda, 1.0 );
    else
    if ( mode == 1 )       // show true texture coordinates
        color = texture ( testMap, tex );
    else
    if ( mode == 2 )       // show interpolated texture coordinates
        color = vec4 ( uv, 0.0, 1.0 );
    else                    // show delta
        color = vec4 ( length ( texture ( testMap, tex ).xy - uv ) );
}

Следующий фрагментный шейдер используется в примере vb-3 и он позволяет сравнить настоящий градиента текстурные координат и рассчитанный.

-- vertex
#version 460 core

layout(location = 0) in vec4 pos;

out vec2 tex;
//out vec2 viewRay;

uniform mat4 proj;

void main(void)
{
    tex         =  pos.zw;
//  viewRay.x   = -pos.x / proj [0][0];
//  viewRay.y   = -pos.y / proj [1][1]; 
    gl_Position = vec4 ( pos.xy, 0.0, 1.0 );
}

-- fragment
#version 460 core

struct  Vertex
{
    float   f [6];
};

layout ( std430, binding = 0 ) buffer Vertices
{
    float   f [];
};

uniform usampler2D visMap;
uniform sampler2D  testMap;

uniform mat4 mv;
uniform mat4 proj;
uniform int  mode;

in  vec2  tex;
out vec4  color;

vec4    getPos ( int triangle, int no )
{
    int index = 3 * 6 * triangle + no * 6;
    
    return vec4 ( f[index + 0], f[index + 1], f[index + 2], f[index + 3] );
}

vec2    getTex ( int triangle, int no )
{
    int index = 3 * 6 * triangle + no * 6;
    
    return vec2 ( f[index + 4], f[index + 5] );
}

void main(void)
{
    vec2    winSize = vec2 ( textureSize ( visMap, 0 ) ); 
    vec2    ndc     = 2*tex - vec2 ( 1.0 );     // convert tex to NDC
    uint    id      = texture ( visMap, tex ).x;
    
    if ( id < 1 )   // skip empty space (with 0s)
        discard;
        
    id--;

        // get triangle vertices 
    mat4    m    = proj * mv;
    vec4    v0   = m * getPos ( 0, 0 );
    vec4    v1   = m * getPos ( 0, 1 );
    vec4    v2   = m * getPos ( 0, 2 );
    vec3    w    = vec3 ( v0.w, v1.w, v2.w );
    vec3    invW = 1.0 / w;

        // compute NDC coordinates of triangle vertices
    vec2    p0 = v0.xy * invW.x;
    vec2    p1 = v1.xy * invW.y;
    vec2    p2 = v2.xy * invW.z;

        // compute 1/D
    float   invD = 1.0 / determinant ( mat2 ( p2 - p1, p0 - p2 ) );

        // compute barycentrics lambda of NDC point (x,y)
    vec3    lambda;

    lambda.x = (( p1.y - p2.y )*( ndc.x - p2.x ) + ( p2.x - p1.x ) * ( ndc.y - p2.y )) * invD;
    lambda.y = (( p2.y - p0.y )*( ndc.x - p2.x ) + ( p0.x - p2.x ) * ( ndc.y - p2.y )) * invD;
    lambda.z = 1.0 - lambda.x - lambda.y;

        // compute gradient
    vec3    lx = vec3 ( p1.y - p2.y, p2.y - p0.y, p0.y - p1.y ) * invD;
    vec3    ly = vec3 ( p2.x - p1.x, p0.x - p2.x, p1.x - p0.x ) * invD;

        // compute gradient of 1/w
    float   diwdx  = lx.x * invW.x + lx.y * invW.y + lx.z * invW.z; // dot ( lx, invW )
    float   diwdy  = ly.x * invW.x + ly.y * invW.y + ly.z * invW.z;

        // compute w at (x,y) by linearly interpolating 1/w
    vec2    delta = ndc - p0;

        // now lerp 1/w to get w at ndc
    float   iwp = invW.x + delta.x * diwdx + delta.y * diwdy;  
    float   wp  = 1.0 / iwp;

    // gives correct lambda
//lambda.x = wp * ( invW.x + delta.x * lx.x * invW.x + delta.y * ly.x * invW.x );
//lambda.y = wp * ( 0.0    + delta.x * lx.y * invW.y + delta.y * ly.y * invW.y );
//lambda.z = wp * ( 0.0    + delta.x * lx.z * invW.z + delta.y * ly.z * invW.z );


        // convert to pixels
    lx *= 2.0 / winSize.x;
    ly *= 2.0 / winSize.y;

        // invert y (Vulkan only)
        //dldy = -dldy;

        // compute w(x+1,y) and w(x,y+1)
    float   wx1 = 1.0 / ( iwp + dot ( lx, invW ) );
    float   wy1 = 1.0 / ( iwp + dot ( ly, invW ) );

        // now compute lambda(x+1,y) and lambda(x,y+1)
    vec3    lx1 = wx1 * ( lambda * iwp + lx * invW );
    vec3    ly1 = wy1 * ( lambda * iwp + ly * invW );

        // and now get final lambda gradients
    vec3    ddx = lx1 - lambda;
    vec3    ddy = ly1 - lambda;

#if 0
ddx = lx;       // works better, WHY ?
ddy = ly;

#endif

ddx = ddx * invW;       // WHY ???
ddy = ddy * invW;

        // now do perspective-correct texture coordinates interpolation
    vec2    tx0 = getTex ( 0, 0 );
    vec2    tx1 = getTex ( 0, 1 );
    vec2    tx2 = getTex ( 0, 2 );
        
    float   den = dot ( lambda, invW );
    vec2    uv  = (tx0 * lambda.x * invW.x + tx1 * lambda.y * invW.y + tx2 * lambda.z * invW.z) / den;

        // compute gradients
    float dudx   = dot  ( vec3 ( tx0.x, tx1.x, tx2.x ), ddx );    
    float dudy   = dot  ( vec3 ( tx0.x, tx1.x, tx2.x ), ddy ); 
    float dvdx   = dot  ( vec3 ( tx0.y, tx1.y, tx2.y ), ddx );    
    float dvdy   = dot  ( vec3 ( tx0.y, tx1.y, tx2.y ), ddy ); 
    vec2  dtexdx = vec2 ( dudx, dvdx ) / den;
    vec2  dtexdy = vec2 ( dudy, dvdy ) / den;

        // find eye-space z
    float   z = (v0.z * lambda.x * invW.x + v1.z * lambda.y * invW.y + v2.z * lambda.z * invW.z ) / den;
    
    if ( mode == 0 )        // show baricentrics
        color = vec4 ( lambda, 1.0 );
    else
    if ( mode == 1 )       // show ddx delta
        color = vec4 ( 10 * length ( texture ( testMap, tex ).xy - dtexdx ) );
    else                   
    if ( mode == 2 )        // show ddy delta
        color = vec4 ( 10 * length ( texture ( testMap, tex ).zw - dtexdy ) );
    else                   // show delta
    if ( mode == 3 )
    {
        vec2 dtdx = texture ( testMap, tex ).xy;
        vec2 dtdy = texture ( testMap, tex ).zw;

        float rho = 10 * sqrt ( max ( dot ( dtdx, dtdx ), dot ( dtdy, dtdy ) ) );

        color = vec4 ( rho );
    }
    else
    {
        float rho = 10 * sqrt ( max ( dot ( dtexdx, dtexdx ), dot ( dtexdy, dtexdy ) ) );

        color = vec4 ( rho );
    }
}

Полезные ссылки:

The Visibility Buffer: A Cache-Friendly Approach to Deferred Shading

Deferred Attribute Interpolation for Memory-Efficient Deferred Shading

Visibility Buffer Rendering with Material Graphs

Triangle Visibility Buffer

The filtered and culled Visibility Buffer

Recreating Nanite: Visibility buffer

My toy renderer, part 3: Rendering basics

I3D 2024 The Forge Industry Talk - Triangle Visibility Buffer 2.0

По этой ссылке вы можете скачать исходный код к этой статье.